信息论与编码
这篇博客是帮忙测试的内容,博客主人关于公式渲染出了一些问题,我放上来进行测试使用
前言
这篇总结和系统性学习地笔记,是基于电子科技大学的《信息论与编码》课程,而我写作的初衷是个人的复习。因此,内容可能不是那么详细,但是我会保证基本上我会在自己理解的基础上,完成这篇文章。随着我自己的理解的加深,可能会出现前后不一致的情况,如果读者感到矛盾,那么请在评论区说明,等我有时间时会继续完善的。
离散信源熵
单符号离散信源是最简单的情况,离散是指信源输出是有限个符号,单符号是指每个符号都是独立的,每次只发出一个符号。
随机变量基础
在单符号离散信源中,每个符号的概率分布可以用一个概率向量来表示。例如,一个三个符号的单符号离散信源可以用以下概率分布表示,符号 A、B、C 之间是相互独立的,即一个符号的出现不会影响到其他符号的出现概率。可以如下的方式抽象成数学模型。
离散随机变量集合:${a_1,a_2,a_3}$,对应概率 $P(a_i)$,且 $0 \le P(a_i) \le 1$ , $\sum{p\left( a_i \right)}=1$.
| 符号 | 出现概率 |
|---|---|
| A | 0.2 |
| B | 0.3 |
| C | 0.5 |
对于二维随机变量,也是有类似的结论,比较特殊一点的是,
对于随机变量独立的情况,可以同时发生可以拆开成乘法,条件概率没有影响。
信息量
在有了概率分布的基础之后,就可以开始学习基于统计的自信息量的概念了。一定记住公式,单位是 bit
需要注意的性质,自信息量的范围是 $(0,+\infty)$,而且是单减函数。
对于联合变量,有联合自信息量,计算公式也是类似的:
特别的,当互相独立时,就可以拆开:
条件信息量则除了计算公式,还和自信息量、联合信息量有直接关系。简单说,就是 a 的信息量+a 已经发生后 b 发生的信息量,就是 a 和 b 同时发生的信息量:
以上,讨论了单个符号的信息量和联合信息量的定义,一个单符号离散信源会有多个符号,就提出了衡量信源信息量的信源熵,简单地说,就是每个符号的信息量的平均值,或者信源的平均不确定度、随机性,单位是 bit/sign:
信源熵
如果同时考虑两个信源,要计算条件熵,可以根据数学期望的定义,得到:
这里必须注意,出现 $I(a_i/b_j)$ 的概率是 $a_i$ 和 $b_j$ 同时发生。也可以用如下的办法推理,一次只考虑一个随机变量:
显然的,因为 $p(a_ib_i)<p(a_i)$ 且 $p(a_i)$
对于联合熵,也是一样的做法。而且类似于联合信息量,和单独的信源熵和条件信源熵有关
而且可以由于信源熵是非负数,可以发现联合信源不确定性更大。
信源熵很重要的性质就是,当信源 X 的 n 个符号,每个符号概率相等时,信源熵取得最大值 $H(X)=\log _2n$,因为
另外值得注意的是,因为 $\lim _{\varepsilon \rightarrow 0} \varepsilon \log \varepsilon=0$ 所以小概率事件实际上对信源熵的贡献比较小。而且信源熵是严格上凸函数。
从信息量的角度,还可以发现 $H(X)\ge H(X/Y)$,这叫做极值性。如果 Y 可能包含了 X 的某些信息,那么信源熵就会减少,除非 Y 是确定的,或者是二者不可能同时存在。这不要求证明。
信道编码
信源发出的消息序列通常不能直接送 给信道传输,需要经过信源编码和信道编 码。信道编码的目的是,提高编码的效率,降低差错,压缩信源的冗余度。简单地说, 编码是一种映射,是将输入符号映射成码字。
根据编码的方式,可以分成无失真编码和限失真编码。很显然的,无失真编码的映射需要一一对应,可逆。因此无失真编码只能用在离散信源,不能用在连续信源。比如说模拟信号转化成数字信号,是无法产生无数种字符(数字),来表示连续的值。
假设这样一个编码过程,离散信源 X 一次产生 L 个字符,也就是每次输出是 ${a_1a_2\dots a_l}$ 这样的序列,这称作 L 元。那么现在要找到一种编码方式,将原来的符号映射成另外一套符号。定长编码定理就是研究这样的编码过程,它提出了,假如编码系统使用的字符有 m 个取值(一般是 2 个,0 和 1),每次输出 k 个符号 $b_1,b_2,\dots,b_k$,也就是定长地用 K 个字符表示一个符号 ${a_1a_2\dots a_l}$,也即
那么,根据定长编码定理,如果要尽可能压缩信息,减少编码的长度 K,但是同时要保证无失真编码,那么一定需要满足:编码后 X 的每个符号对应的编码携带的最大信息量,大于 X 的信源熵。下面的 $\ln m$ 就是编码后的最大信源熵,R 称作信息率。
其中,又定义的编码效率:
变长编码定理则告诉,如果编码的平均长度满足下面的条件,那么一定存在无失真编码,而且信息率 R 大于信源熵:
在变长编码定理的框架内,还需要一种系统的编码的方式,确保在变长的码字不会产生歧义,而且接收序列时可以立即匹配编码,不用观察后面的码字。
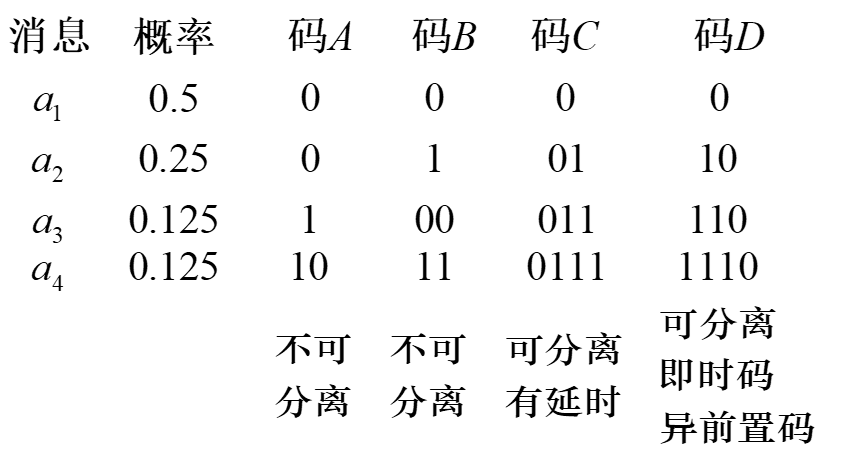
根据克拉夫特不等式,能够找到这样的异前置码编码方式的充要条件是,对于 m 个字符的编码系统,信源 X 的每个字符映射后的字符长度 $k_i$,满足:
香农编码
香农编码就是这样变长编码的一种方式。按信源符号的概率从大到小的顺序排队,然后对每个字符定义累加概率(排在它前面的字符的概率之和),这样就可以得到结论:
编码则是 $p_a\left(a_j\right)$ 二进制表示的小数点后 $k_i$ 位。参考下面的例题。
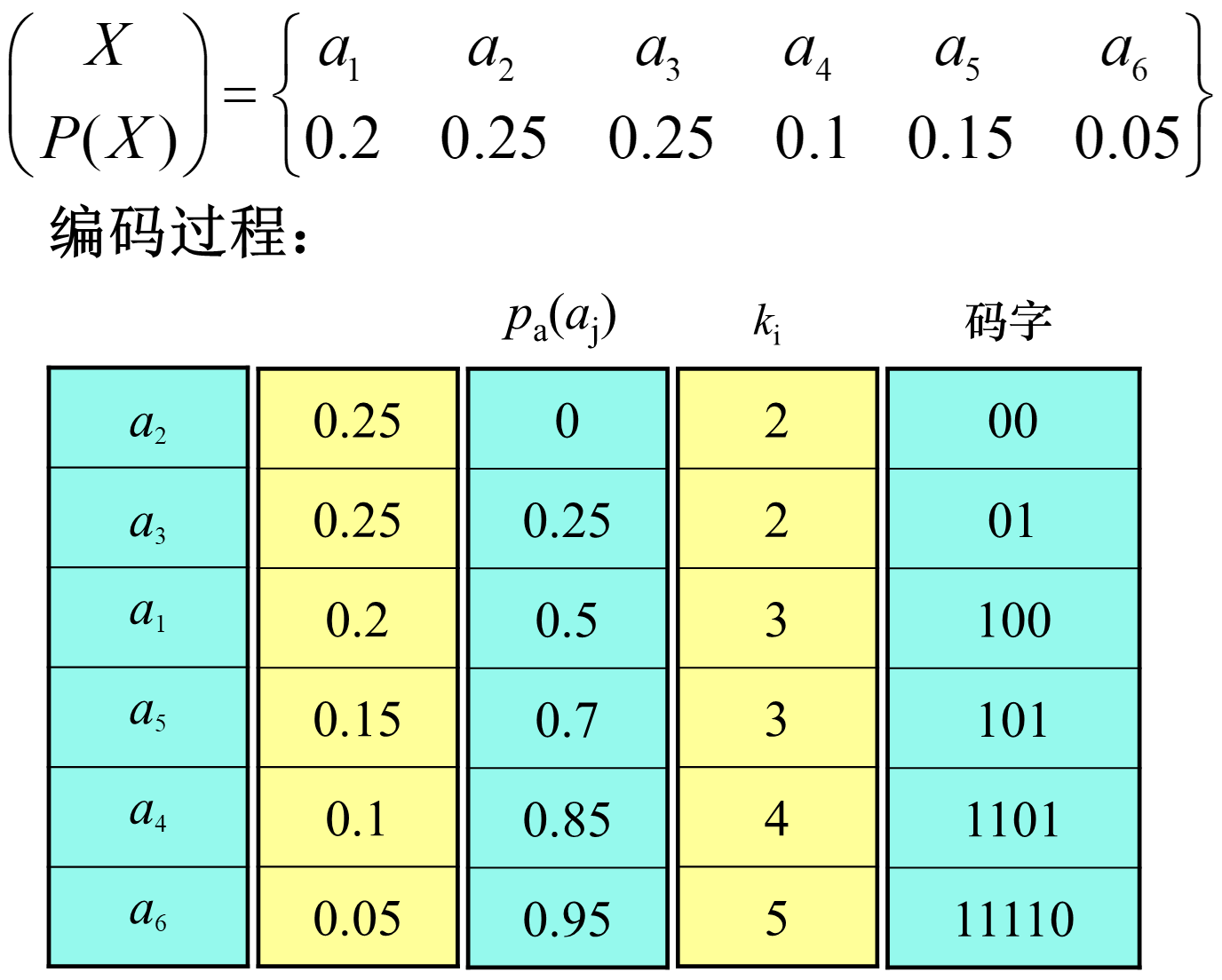
可以计算得到相关参数:
费诺编码
首先从大到小排队,然后把符号分成 2 组,要求这是所有分成 2 组的情况中,每组概率之和相差最小的情况。然后随意给两组其中一个分配 0,另一个分配 1。每组内部继续按照上面的规则分组和编码。
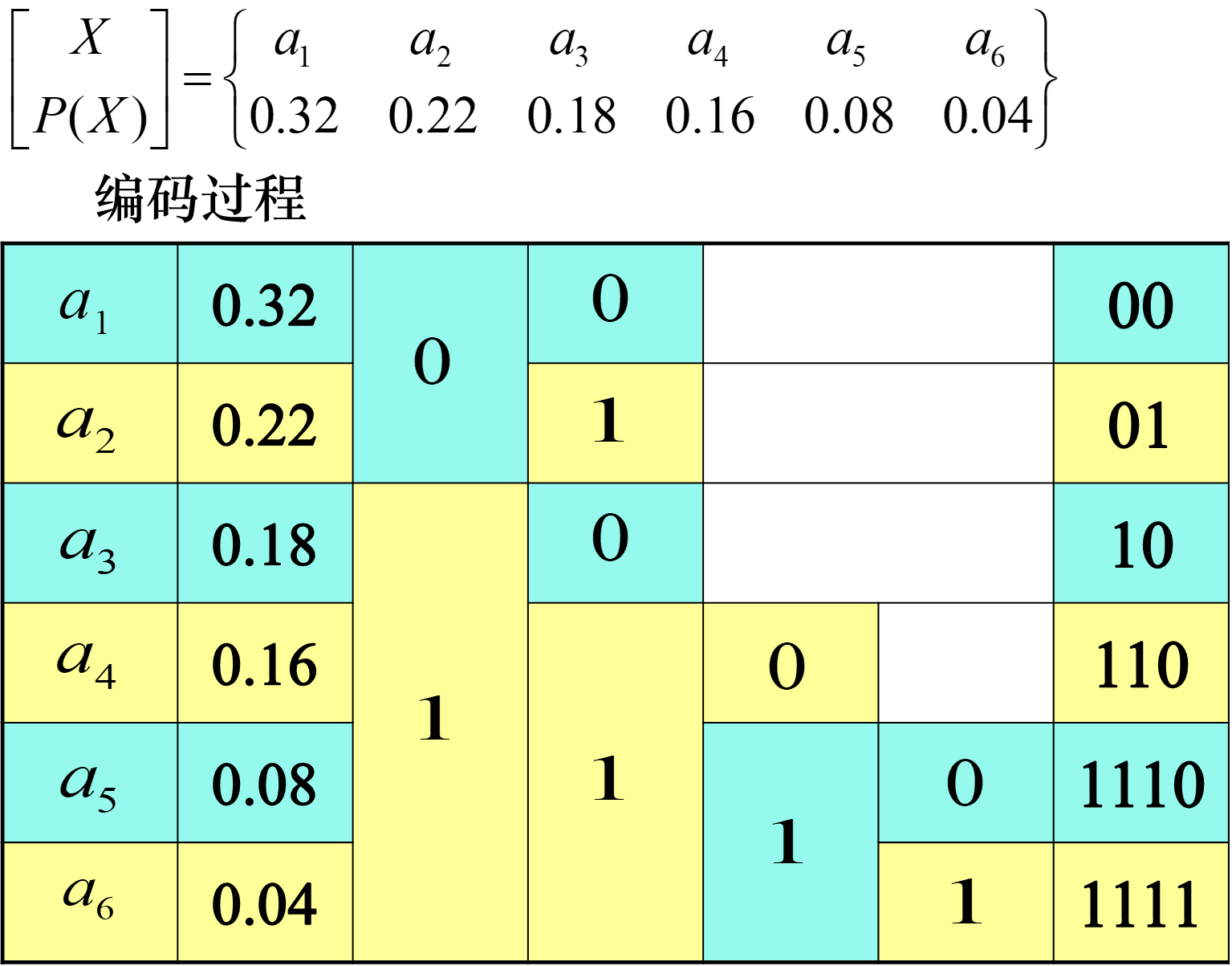
赫夫曼编码
首先从大到小排队,对于符号的概率的 n 种取值,开始构造二叉树,节点时最小的 2 个符号,父节点是他们的和。然后用父节点替代它们,变成 n-1 个符号,去除了之前两个概率最小的符号的概率,增加了一个父节点的概率。重复这个过程,直到只剩下 1 个符号。
下面的序号是代表合并的步骤。

信道容量
信道模型
信道容量(channel capacity)则是指一个信道在特定条件下(例如,特定的信噪比)能够传输的最大信息速率,反映了在单位时间内能够通过信道传输的最大信息量。这里我们不考虑两个信源之间的具体转换关系,而是考虑两个随机变量之间的信息共享量,或者说,一个随机变量中包含的关于另一个随机变量的信息量。这就是互信息量。它也可以衡量特征和目标变量之间的相关性。
直观地讲,如果 X 和 Y 是独立的,那么他们的互信息就是 0,因为知道 X 的值并不能给我们提供关于 Y 的任何信息,反之亦然。另一方面,如果 X 和 Y 完全相关(也就是说,如果我们知道了 X 的值,那么我们就可以确定 Y 的值),那么他们的互信息量就等于 X(或 Y)的熵。
总之,X 和 Y 之间的互信息量或者说相关性,来自信息的传递,如果没有信息从信道传递,那么就是相互独立的。
互信息量
两个随机变量的某个取值,来自 Y 的取值 b 对来自 X 的取值 a 的互信息量,也就是在已知事件 b 发生后,对事件 a 的不确定性减少的程度,
定义如下:
这个定义体现了通过信宿 Y 的值 b 来推测信源 X 的值 a,与实际信源 X 的值 a 的概率的比值,也是这一次传输的信息量。如果事件 b 发生了,那么我们对事件 a 的预测可能会更准确一些,也就是说,事件 a 的不确定性可能会降低。而造成这种不确定性的减少的原因,就是信源 X 通过信道传递信息到了信宿 Y。
从自信息量的角度,也可以验证刚才对互信息量的解释。因为在信息传递之前,信源 X 和信宿 Y 是独立的,只有信息传输之后,才会有共享的信息。传递的部分就是信源 X 的信息量,减去从信宿 Y 获取观察信源 X 的信息量:
如果从信息共享(也就是信息传递)的角度看,更加直观的形式如下:
通过简单变形,就有了最开始互信息量的定义,它给我们提供了一种,不知道 $p(b)$ 但是知道 $p(a|b)$ 的情况下的计算方法。
对于两个信源而言,平均互信息量就是所有组合的互信息量的平均值:
注意:
互信息量是可以为正,也可以为负。
但是平均互信息量是非负数。相互独立的时候有 $p(ab)=p(a)p(b)$
当 X Y 独立的时候,共享的信息为 0,平均互信息量为 0.
共享的信息,无论从 X 的角度还是从 Y 的角度,都是相等的
- 共享的信息量不可能超过信源本身,也就是极值性。当 X 和 Y 一一对应就是无损的信道:
平均互信息量是 $p(a)$ 的上凸用函数,$p(b|a)$ 的下凸函数。
信息传递递减。假设 X Z 互相独立,经过 Y 传递信息,那么
条件互信息量
特别地,教材里还提到了条件互信息量,信源 X 和信宿 Y 都知道一个条件 c,那么定义在条件 c 下的 a b 的互信息量为:
这里要稍微注意的是,条件互信息量的表示,容易有歧义。c 是共有的条件。特别的,如果把 b c 所在的信源作为一个整体,a 所在信源作为信宿,有:
这也比较直观,从 b c 传递给 a 的信息,来自于从 c 传递给 a 的信息和 a b 已知 c 的情况下,b 给 a 传递的信息。
平均互信息量的三个视角
从信息传递的角度看,可以分别从信源 X 的角度、信宿 Y 的调度和通信系统整体的角度,看待平均互信息量(传输的信息量)和信源熵(信源传输信息的能力)。
从信源 X:
这表示 X 发送信息后,从 X 观察 Y,Y 剩下的不确定度,也就是信息熵。
从信宿 Y:
这表示 Y 接收信息后,从 Y 观察 X,X 剩下的不确定度,也就是信息熵。
从通信系统:
这表示原本传递信息之前,X 和 Y 是独立的,提供的信息熵为 $H\left( X \right)+ H\left( Y \right)$。但是当 X 和 Y 通信后,X Y 作为整体所提供的信息熵就变成了 $H\left( XY \right)$,二者之差就是传递的信息量。
信源熵互信息量的关系
下面的图中,$I(X;Y)$ 表示 X Y 重叠部分,$H(XY)$ 表示两个圆的组合,$H(X/Y)$ 表示圆 X 挖去了圆 Y 的部分。


单符号离散信道容量
仍然假设输入$X\in { a_1,a_2,\cdots a_n } $,输出 $Y \in{b_1, b_2, \cdots b_m}$,那么信息从 X 传递到 Y 的转移概率矩阵,也叫做信道矩阵如下:
信道容量通过调整 $p(a_i)$的概率分布,实现 X 和 Y 最大的互信息量,也就是最大的可以承载的能力。
一般的信道容量是比较复杂的,只需要掌握特殊的即可。很多时候入门信息论,都是定性分析。优化的变量,都是 X 的符号的概率,而不是 Y 的概率。
无噪声 X 和 Y 一对一:
那么转移概率矩阵就是每行一个 1,而且每列一个 1,那么 $H(X|Y)=H(Y|X)=0$
无噪声 X 和 Y 一对多:
信道矩阵就是每行若干个概率,但是每一列只有一个不为 0
那么 $H(X|Y)=0$ 但是 $H(Y|X)\ne 0$,而且 $H(X)<H(Y)$
无噪声多对一:
类似于 $a_1 \rightarrow b_1$ $a_2 \rightarrow b_1$,所以信道矩阵如下:
这样就有 $H(Y|X)=0$,所以
强对称:
对于信道 ${ X\,\, P\left( Y|X \right) \,\,Y } $ ,输入和输出的符号种类数量相同,而且每个符号传递对应传递的概率为 $1-p$,其他传递错误的可能性平分。每一行和每一列都是 1。也就是如下
那么很特殊的性质就是 $H(Y|X)$ 是常数,因为每一行信源熵都相等,所以
令这个常数为 $H_{ni}$,就得到了下面的结论
$H_{ni}$ 随着 p 变化的函数图像如下:
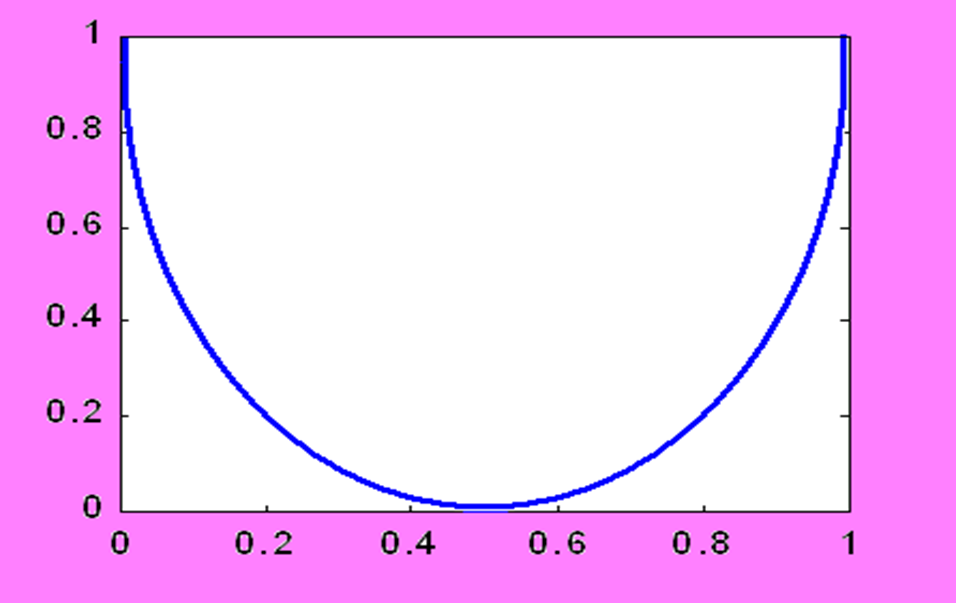
最后,当整个信道矩阵都是 $\frac{1}{n}$ 的时候,取到最大。具体过程忽略
对称:
对称信道和强对称信道有类似之处,但是条件更加宽松,只需要每一列是同一个集合的排列,每一行也是同一个集合的排列,不再需要 $a_i \rightarrow b_i$,也不需要错误映射的可能性平分。
这样就会出现有趣的性质,因为每一行的和为 1,假设是 ${q_1,q_2,\cdots,q_n}$ 这 n 个可以重复的元素,那么每一列都包括了其中一个元素,那么如果 m
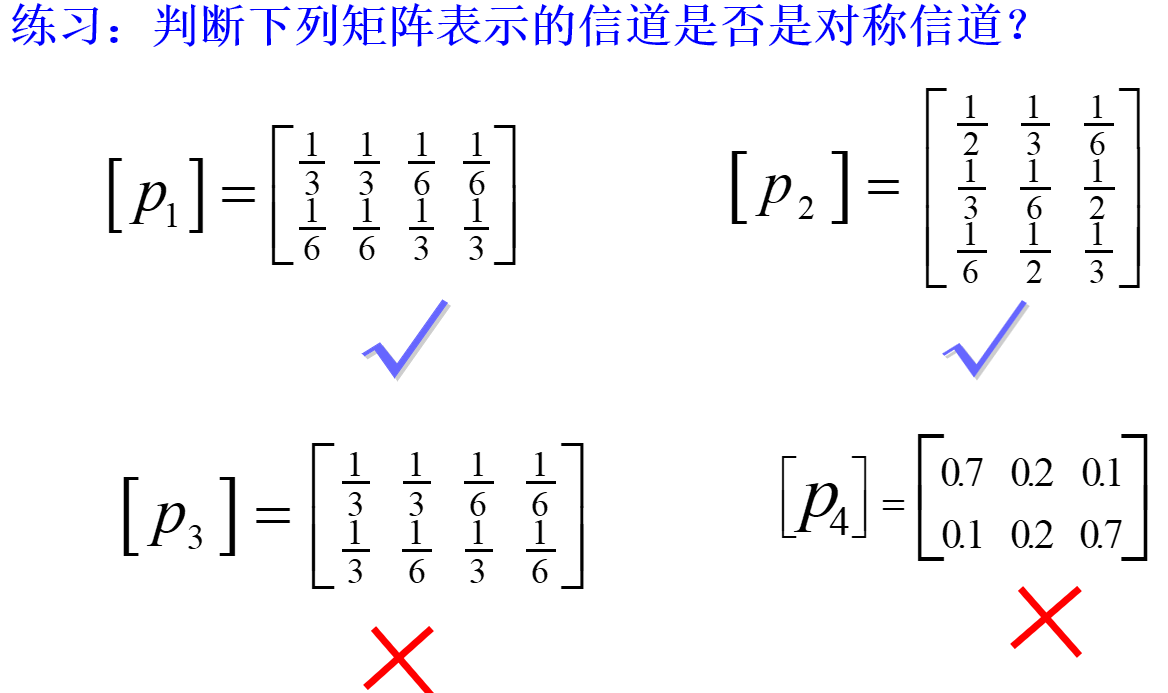
对于这样的信道矩阵,可以明显知道,每一行的信息量是相等的,也即
可以发现,和强对称矩阵不一样了,虽然取等条件也是X每个符号等概率,但是最大值是由 Y 的符号个数决定了。
准对称矩阵:
每一行都是同一个集合的排列,列不是。但是列可以通过分组,把原来的 n*m 的矩阵,分组成 这个 s 个矩阵。
(待续)
(不写笔记了,这门课很多概念就是没有搞清楚,课程要求也是会背公式,计算就可以了。我去理解原理反而有害分数,而且非常费力。)
下面是另外一部分需要测试的内容
最后,总结一般流程:
- 确定状态集合: $D$ 是每个子状态或者元素的定义域。
- 每个执行路径上的每个节点视作状态集合 S 的元素。
- 确定初始值状态 ,设置执行路径上每个节点的状态默认值 $DATA_{node}=\left( T,T,T,\cdots \right)$,$T$ 表示任何情况,随后的半格理论中会再次说明。
- 确定节点的状态转换函数 $f_v:\boldsymbol{S}\rightarrow \boldsymbol{S}$,具体的函数规则由每个节点的内容决定。
- 在控制流汇合处,例如在节点
v处回合,确定交汇运算 ,其中 $v$ 表示当前节点,$pred(v)$ 表示当前节点的前驱节点的集合,所以 $w$ 指的是前驱节点。我们约定,交汇处会覆盖默认值,也即 。$\Pi$ 表示交汇运算。