来自Guuuuuu老师的CV岗、OCR、目检检测、多模态方向面试经验分享
该面经来自Guuuuuu老师儿,浙江大学软件学院研究生,在人工智能上十分优秀,Gu老师的CRNN和CTPN教程对我十分有帮助
自我介绍
略
项目问题
简历项目
面试问题
问过的基础问题
DBNet的都用了哪些loss
BinaryCrossEntropy(prob map, binary map) L1 (threshold map),但是代码实现中有对binary map采用Dice loss,即对预测map和gt map计算该公式 ,这里其实是借鉴了PSENet中的做法,他认为文字只在图片中占很小的区域,因此正负样本不均衡,相当于负样本多,使用BCE loss容易让网络偏向预测非文字区域,而Dice loss恰好对正负样本不均衡的场景有比较不错的性能,训练过程中更侧重对前景区域的挖掘(缺点是对反向传播不利,训练loss不稳定,尤其是小目标)DBNet为什么做shrink操作
shrink为了更好区分实例,直接分割可能紧密的文字会被检测成一个连通区域,分割方法比较敏感,借鉴自PSENetHard Negative Mining
先划分正负样本1:3训练,训练好的模型预测剩余的负样本,把预测成正样本概率大于某一阈值的负样本挑出来加入训练集有利于模型的训练,相当于加入错的比较厉害的样本让网络学习,RCNN方法中常用。例如厨房预测蜘蛛的例子,含有蜘蛛的图片可能很少,但是厨房可能有很多东西长得像蜘蛛,拿这些负样本训练有利于模型学习更好的特征Attention都有哪些方式
本质上就是加权求和,主要就是计算权重
Encoder-Decoder机制角度
解决长序列仅依靠一个context解码,所以加入attention
朴素attention: decoder每次输入上一个时间步的预测输出,得到hidden vector作为q,encoder的每个time step的hidden vector作为k,v,计算权重相似性相关性(点积,cosin相似性,MLP加点可学习参数预测),计算权重(softmax),加权求和得到当前time step decoder的一个context然后和hidden vector concat预测当前时间的输出
self attention: 序列的每个token embedding线性映射得到QKV,然后每个Q对所有的K计算相关性权重,然后对V加权求和得到当前位置的这个attention特征
- 多头self attention: 与其说做单个的注意力,不如把每个QKV投影到低维投影多次,每个embedding得到多个QKV,最后得到的attention 特征并在一起在做一个投影回到原来的尺寸。为什么做多头,比如Transformer里面,可能计算相似度的时候直接使用点积没什么可学习的参数,有时候为了识别不一样的模式,其实这里多次投影就是学到不一样投影的方法,使得在投影进去的那个空间里面可以度量不同的模式(from 李沐 Transformer论文精读)
特征图角度的Attention机制
也是做加权求和,主要是求权重
- 特征图:以CBAM为例,我一个特征图可以保持channel维度不变把WH维 度pooling成1,然后经过MLP求一个权然后做Channel维度的attention,然后可以保持WH维度不变,对Channel维度pooling然后经过几层卷积得到WH维度的权重,然后对WH上做空间attention
- 多尺度:给FPN不同尺度上加自适应的权重,去学习,相当于做不同阶段feature map的attention
- Transformer中做self attention时,求softmax的公式为什么要给logits除 ,d是维度
简单来说为了稳定梯度。因为做self attention求相关度的时候要做点积,而当d比较大时,有时可能使得值会非常大,当值变大时,和其他值的相对差距也就会变大,使得softmax做出来会非常接近1,其他值就会接近于0,当出现这种情况时,算梯度会很小,因此除一个根号d是个不错的选择,实验可以发现,对于d比较大时,scale后的softmax求梯度可以比较稳定,而不带scale的softmax很容易梯度消失。
具体的一些数学解释可以看:https://www.zhihu.com/question/339723385
Focal loss如何解决正负样本不均衡的
CE loss前面加权重 $(1-p_y)^\gamma$,当预测正确是$1-p_t$这个权重接近0,降低loss权重,而预测错误时, $1-p_t$接近于1,相当于原始的CE loss。 相当于对于样本难易程度的控制,即怎么算难样本怎么算易样本。外面再套一个balance参数,正样本a负样本1-a(a可以用类别频率的倒数或当成可调超参数,进一步给不均衡的正负样本做加权)SVM
详细讲解视频B站《机器学习白板推导》https://www.bilibili.com/video/BV1aE411o7qd?p=28
svm有三宝:间隔,对偶,核技巧
分类:硬间隔svm,软间隔svm,核svm
- 硬间隔svm:(最大间隔分类器)对线性可分问题
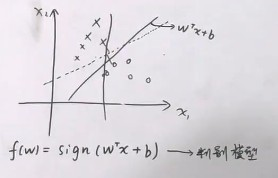
可以分隔两类的超平面很多,但是要找到一个超平面使得它到样本点的距离都足够大
margin定义为点到超平面距离,最小的那个
借助拉格朗日乘子将带约束问题变成无约束问题
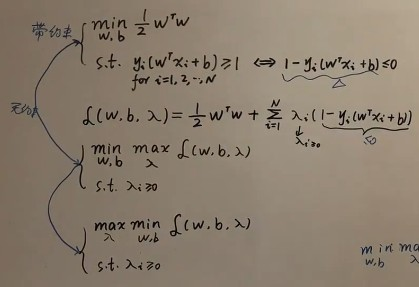
然后求其对偶问题
对偶问题的关系(下面是弱对偶关系)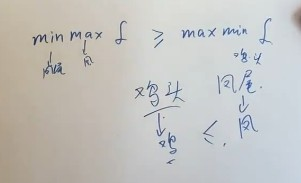
相等时强对偶关系,而这里的问题本身是强对偶关系,所以直接求其对偶问题
KKT条件
原问题和对偶问题是强对偶关系的充要条件是KKT条件

只在支持向量(两条虚线)上lambda才有值,其他都是零,解其实可以看成是数据的线性组合
- 软间隔svm:
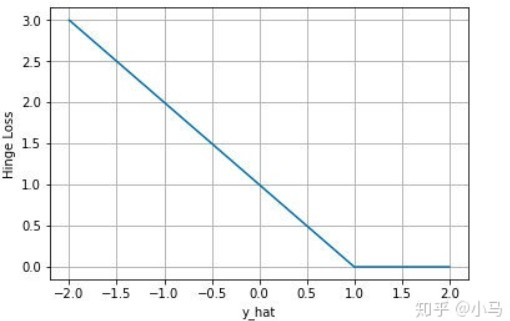
硬间隔认为数据理想线性可分,实际情况复杂软间隔的思想就是允许有一点点错误,引入hinge loss

- 核svm(针对严格非线性问题):
$\phi(x)$+hard margin
高维比低维更易线性可分
但是求核方法(从思维角度)的值再求内积计算量大,希望有一个函数直接代替求出 内积(核函数,从计算角度)

- Hinge Loss
- c树模型
内容比较多,建议系统学习 - 带有warmup的cosin学习率更新
- yolo系列模型(v1-v5 + X)
建议看看论文,详细学习一下 - Batch Normalization(重要☆☆☆☆☆)
BN解决的问题是对于深层神经网络,隐藏层出现internal covariate shift,即随着隐层参数不断更新,每一层的输入分布会不断变化,导致收敛变慢而且不稳定,本质是因为分布会逐向
非线性激活函数上下限两端靠近,比如sigmoid,会偏向大的正值或负值,这样导致反向传播时底层神经网络梯度消失。
而BN首先就是将每一隐藏层输入的分布拉回到均值0方差1的标准正态分布,但是这样严格限制了网络的表达能力,因此加入beta和gamma两个可学习的参数让数据分布的自由度更高。
- $M \times L$维度的1D数据,M为batch size,L为特征维度
以普通的一维数据为例,每个样本有L个特征,共M个样本,那么它的BN公式表示如下:
对第i个特征,计算所有样本的均值和方差,然后对每个样本的i号特征计算BN如下所示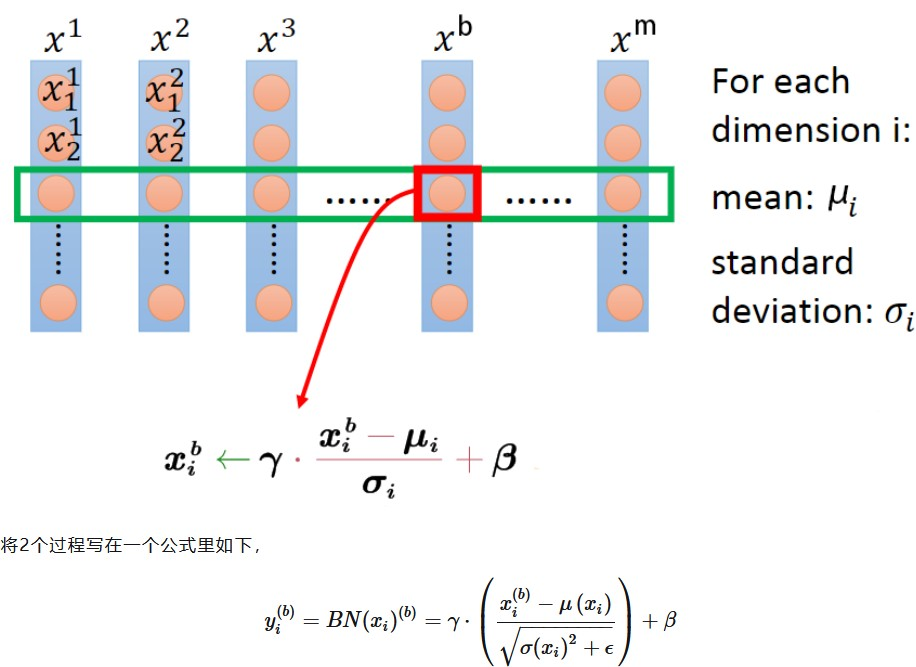
可以看到$\gamma$ 和$\beta$ 如果恰好等于批量的方差和均值时,则等价于没有
BN预测阶段,因为$\gamma$ 和$\beta$ 都是可学习的参数,因此到预测阶段就固定了所以直接拿来用
重点是均值和方差怎么办,因为预测时样本数为1不能计算均值方差,因此需要在训
练阶段计算均值方差的滑动平均值
即使用一个动量参数
1 | running_mean = momentum * running_mean + (1 - momentum) * x_mean |
完整代码如下:
注意,这里的代码求mean和var的部分只适用于 $M \times L$的数据,M为batch size,L为特征维度
1 | def Batchnorm_simple_for_train(x, gamma, beta, bn_param): 2 |
对于 $M \times L$ 的数据,计算mean和var的核心代码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20# 一维数据 N X L N为batch size L为特征数
# pytorch 版本
a = torch.randn((3, 4))
print(a)
mean = a.mean(0) # 按照N维度,对每个特征竖着求mean和var
print('mean:', mean)
var = a.var(0)
print('var:', var)
norm = (a - mean) / (torch.sqrt(var) + 1e-7) # 这里其实运用了 广播机制
print(norm)
# numpy 版本
b = np.random.random((3, 4))
print(b)
mean = b.mean(0)
print('mean:', mean)
var = b.var(0)
print('var:', var)
norm = (b - mean) / (np.sqrt(var) + 1e-7) # 这里其实运用了广播机制
print(norm)
- $N \times C \times L$ 的数据
这种情况其实可以想象成对序列数据做BN,比如NLP中以句子作为输入,C就是每个word embedding的特征维度,L是长度,N是batch size
这里我们假设batch里每个样本即每个句子长度一样,则如下图,其实还是对每个特征做norm,即在C的维度上做norm
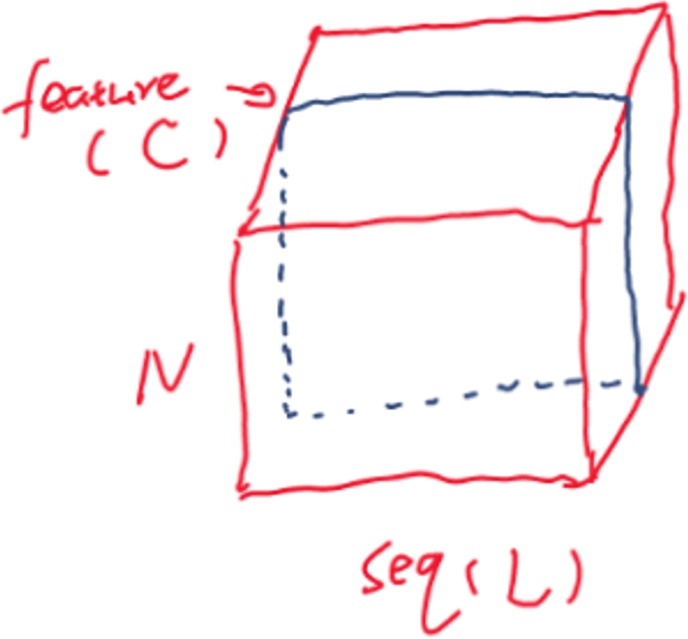
核心求mean和var的代码
1 | # 对 N X C X L 的数据 对C做norm |
- $N \times C \times H \times W$维度的数据
这里主要是BN在CNN上的应用
仍然按照C的维度,对逐个channel计算BN,即有多少个channel就会有多少组可学
习的$\gamma$ ,$\beta$
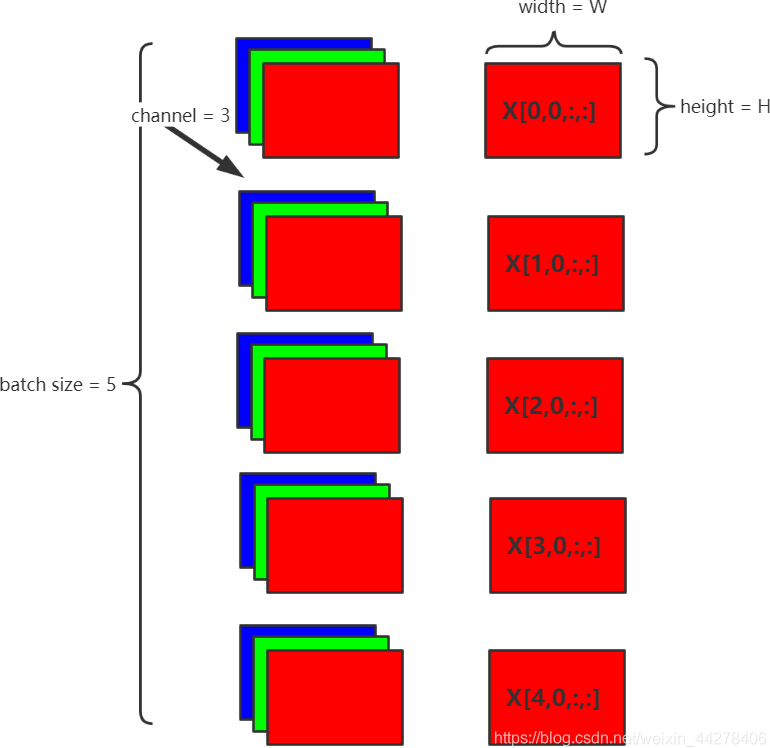
对每个channel计算均值即全部加起来,除以$N \times W \times H$

为什么按照channel维度逐个channel计算BN
其实本质上是对每个feature map做BN,每层有多少个卷积核,就会对应多少的channel,因此对应了多少feature map,就学习几个 ,意味着对每一个卷积kernel得到的batch_size张feature map做一次BN。 求mean和var的核心代码如下:
1 | # 对 N X C X H X W 的数据 对C做norm |
- BN的优点:
- 可以使用更大的学习率,训练过程更加稳定,极大提高了训练速度。
- 可以将bias置为0,因为Batch Normalization的Standardization过程会移除直流分量,所以不再需要bias。 3. 对权重初始化不再敏感
- 深层网络可以使用sigmoid和tanh了,理由同上,BN抑制了梯度消失。
- Batch Normalization具有某种正则作用,不需要太依赖dropout,减少过拟合。
BN的缺点:
batch normalization依赖于batch的大小,当batch值很小时,计算的均值和方差不稳定,因为基于小样本计算的均值方差不能反映全局的统计分布信息,不适用在
- LayerNorm(考Transformer的时候会和BN作对比)
BN存在两个问题
- BN与batch size
当样本数小时不适用,因8为少样本计算的均值方差不能反映全局统计分布信息,方差均值会不稳定。 - BN与RNN:
对于输入是时序序列时,每个样本长度不同,得到的特征可能是如下图所示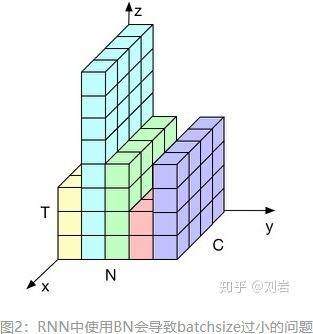
如果我们把这个东西填充成立方体,即其余部分用0填充,batch norm做的事情是下
图这个样子,在这个维度上求均值方差做BN
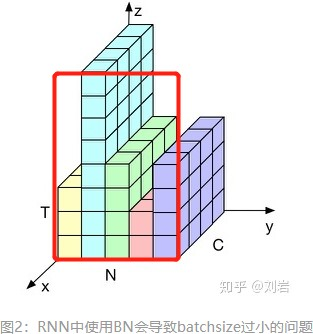
LN是对每个样本做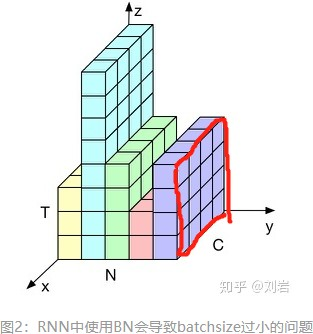
这样做的好处是相比于BN,因为每个样本长短不同,因此计算出来的均值方差会有
较大抖动,此外因为BN需要通过滑动平均计算全局的均值方差用于预测,当预测时
有一个非常长的序列,长过所有训练样本,此时计算的全局的均值方差可能就不太适
用
而LN每次是对一个样本计算均值方差就不存在这个问题
下面是李沐在讲解transformer时对比BN LN的图
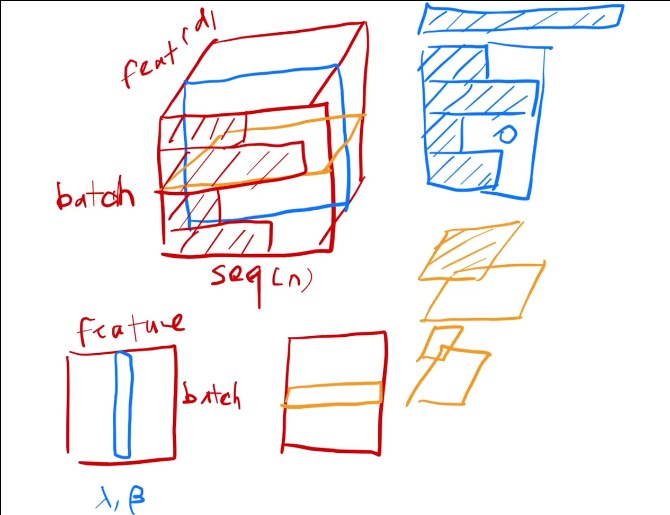
下面是另一个对比图
BN如右侧所示,它是取不同样本的同一个通道的特征做归一化;LN则是如左侧所示,它取的是同一个样本的不同通道做归一化。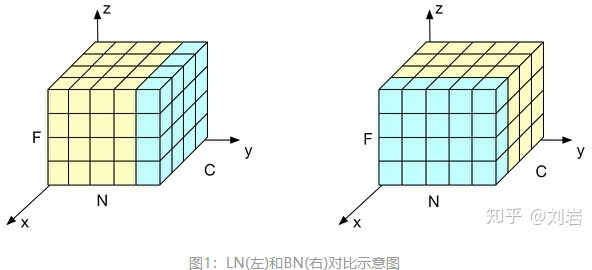
- 二分类为什么不能用MSE Loss
主要原因在于MSE Loss(mean-squared loss)当与Sigmoid搭配使用时,loss的偏导数的变化趋势和预测值及真实值之间的差值的变化趋势不一致。梯度弥散(即在接近负无穷和正无穷时梯度接近于0)

使用Cross Entropy 的梯度信息大于MSE 即收敛速度快
- 深度学习常见回归Loss对比总结(L1, L2, Smooth L1)
- L1 Loss 平均绝对误差(MAE)
其导数为±1,如下图
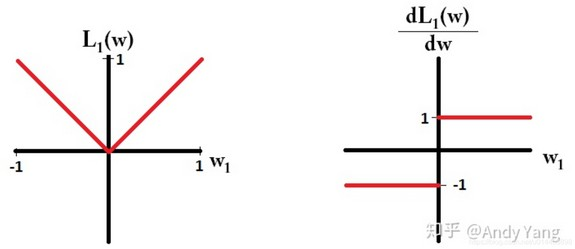
优点:鲁棒性和抗干扰能力更强,对异常点不太敏感,导数稳定不会导致梯度爆炸
缺点:导数恒为常数,收敛慢,很难收敛到高精度
一般用于简单模型
L1 Loss在不可导处如何处理?
坐标轴下降法:

坐标轴下降法进行参数更新时,每次总是固定另外m-1个值,求另外一个的局部最优值
- L2 Loss 均方误差(MSE)
导数为
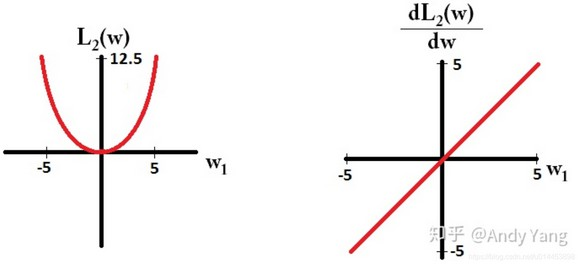
优点:收敛速度比L1 Loss快,稳定性更好
缺点:对异常点敏感,平方会放大误差,输入值较中心值较远时可能导致梯度爆炸一般用于复杂神经网络如CNN
- Smooth L1 Loss
是L1 Loss和L2 Loss的结合体
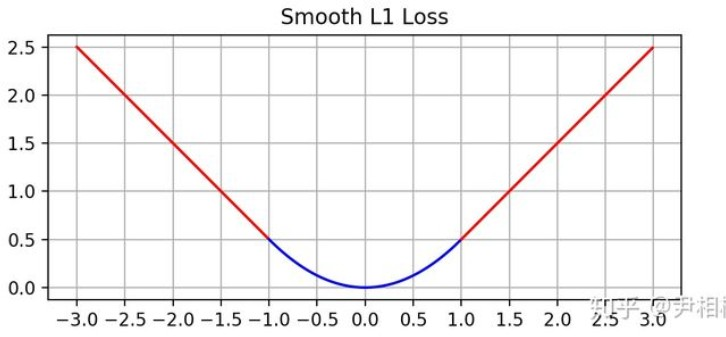
当预测值和ground truth差别较小的时候(绝对值差小于1),其实使用的是L2Loss,当绝对值差小于1时,由于L2会对误差进行平方,因此会得到更小的损失,有利于模型收敛。而当差别大的时候,是L1 Loss的平移,因此相比于L2损失函数,其对离群点(指的是距离中心较远的点)、异常值(outlier)不敏感,可控制梯度的量级使训练时不容易跑飞。在Faster R-CNN以及SSD中对边框的回归使用的损失函数都是Smooth L1 作为损失函数
Smooth L1能从两个方面限制梯度:
- 当预测框与 ground truth 差别过大时,梯度值不至于过大;
- 当预测框与 ground truth 差别很小时,梯度值足够小。

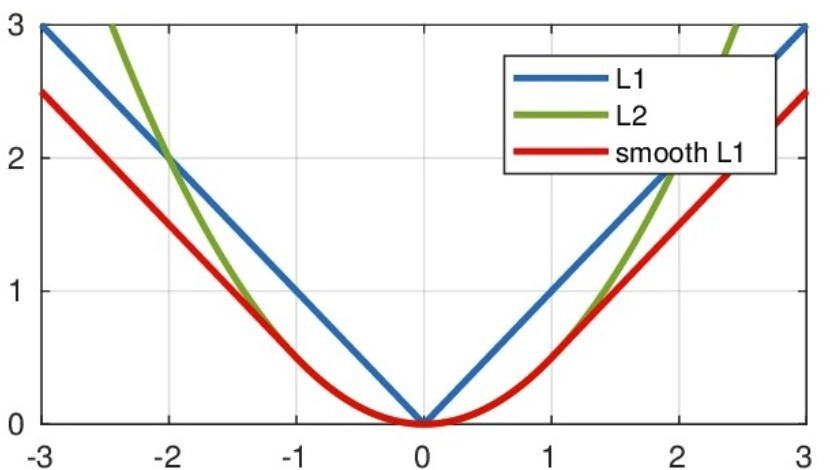
Smooth L1通用形式:
另外,现在主流的实现方式,参考https://github.com/facebookresearch/maskrcnn-benchmark
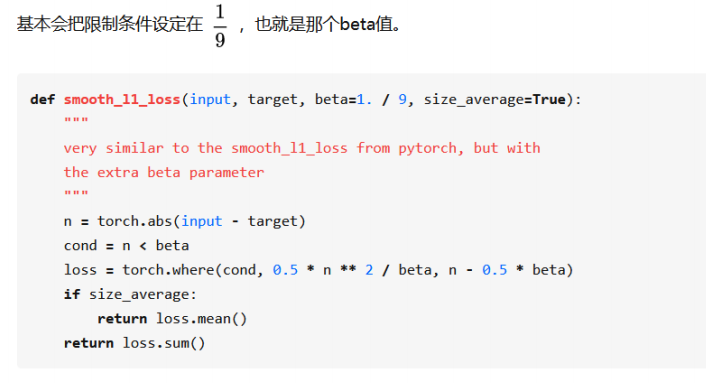
- Cross Entropy Loss
- 二分类
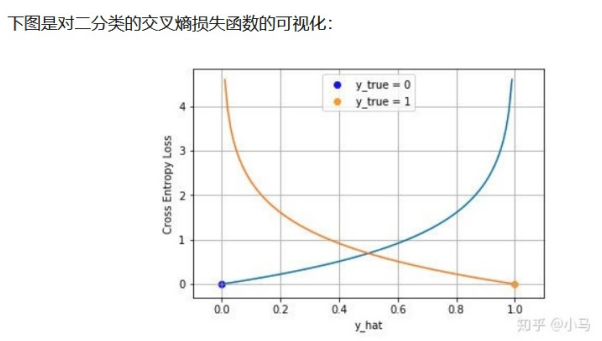
二分类时Cross Entropy Loss就是Logistics Loss,通常会使用sigmoid架构模型的输
出压缩到(0, 1)之间
sigmoid公式
其导数为$S(x)(1-S(x))$
- 多分类
会把sigmoid函数换成Softmax函数,因此多分类时的Cross Entropy也被称为Softmax Loss
softmax公式
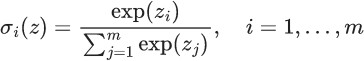

二分类中,使用CE loss和BCE loss模型结构的设计上有什么不同
BCE loss使用sigmoid激活,最终的输出只有一个输出值(一个神经元),CE loss使用softmax需要两个输出值(两个神经元)分类问题为什么使用交叉熵
假设对所有样本 存在最优分布 真实的表示各个样本属于每个类别的概率,那么我们就希望模型输出的 逼近这个分布
然后就用KL散度衡量两个分布的相似性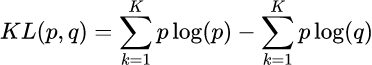
第一项为分布p的信息熵,第二项为分布p和q的交叉熵,将实际的最优分布 和输出分布带入得到: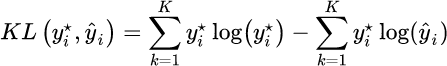
因为前一项和最优分布本身有关,所有变成优化后面一项,形式上就是交叉熵的计算公式
多分类下为什么使用softmax而不是使用其他归一化方法
1.希望特征对概率的影响是乘性的
2.与cross entropy结合反向传播求导形式简洁如何解决softmax的指数上溢下溢问题

- RoI Pooling和RoI Align
RoI Pooling
roi pooling先映射到feature map上得到一个区域,如果输入2x2,首先进行section划分得2x2的区域,然后对每个section取max pooling,具体操作就是行列数/section的行列数得到每个区域几个格子
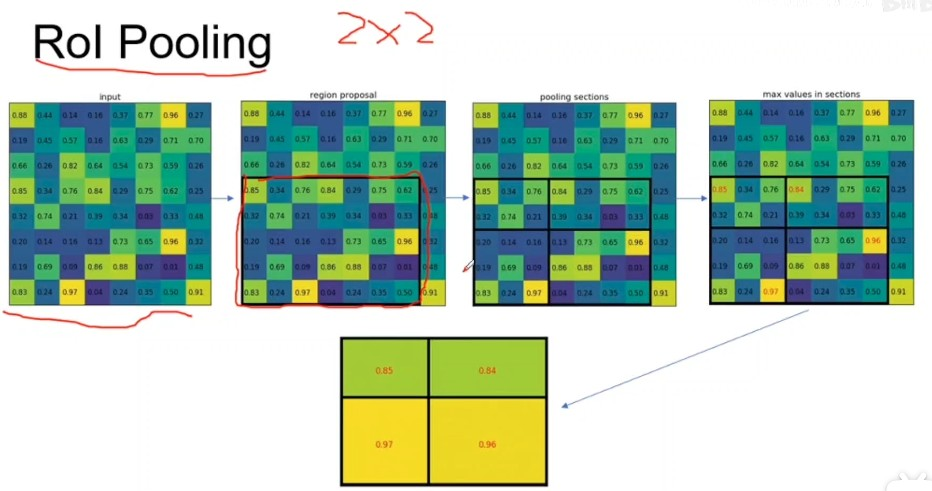
RoI Align
roi pooling映射roi和划分区域的时候取整了这样使得roi和proposal无法对齐,roi align就是要保留浮点数边界,划分的时候也是保留浮点边界,均匀等分。对每个划分完的小区(bin) 域再划分采样点,4个效果比较好,每个采样点通过双线性插值的方法获得,最后对采样点取max pooling
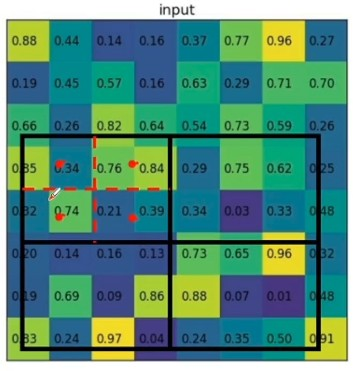
- Anchor生成
在图像左上角创建一组anchor base,首先确定中心点坐标,比如,如果base_size设置为16,我们让中心点为(8,8)
然后创建好数组,大小为ratio长度乘scales长度
两个for循环遍历ratio和scales,然后计算每个ratio和scale下的宽高,宽高计算公式为base_size * scale * sqrt(ratio)和base_size * scale * sqrt(1/ratio)
根号的目的是保证宽高比不被平方
然后根据计算出来的宽高和中心点坐标计算每个anchor左上角和右下角坐标
然后根据feat stride生成在原始图片上的xy坐标偏移量加到anchor base上得到全图的anchor xy坐标偏移量一般是先单独生成一维的x和y的偏移,然后组合成二维网格的偏移,最后xy各重复两遍构成4个元素的元组作为xmin ymin xmax ymax的偏移加上去(具体看源代码)
- Max Pooling如何梯度回传
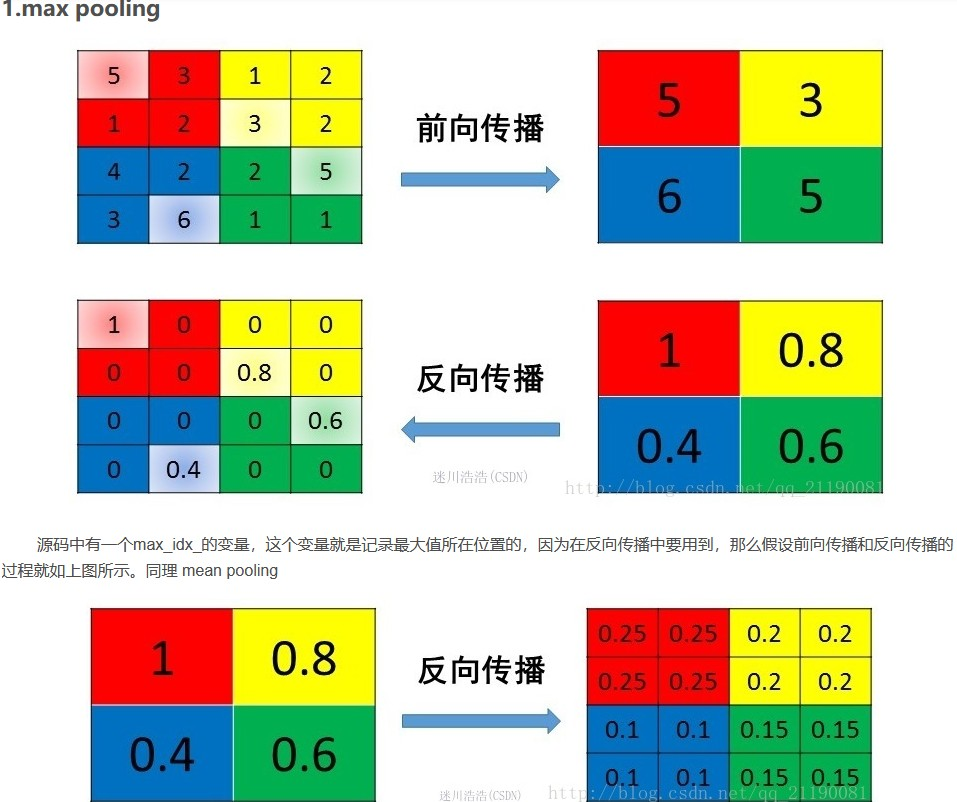
Pooling的作用
(1)下采样,提高感受野
(2)减少参数量,减少过拟合,降低计算成本
(3)可以多尺度融合
最大池化保留了纹理特征,平均池化保留整体的数据特征YOLOv2中anchor聚类的过程
https://zhuanlan.zhihu.com/p/109968578?utm_source=wechat_sessionTriplet loss
Triplet loss最初是在FaceNet的论文中提出,可以较好地学到人脸的embedding,相似的图像在embedding空间里是相近的,可以判断是否是同一个人脸
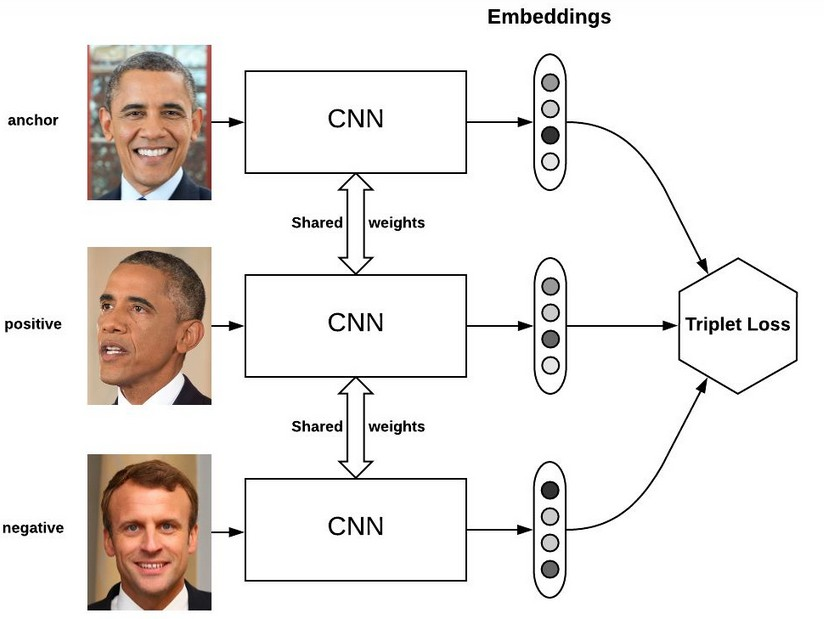
为什么不用softmax 函数呢,softmax 最终的类别数是确定的,而Triplet loss 学到的是一个好的embedding ,相似的图像在embedding 空间里是相近的,可以判断是否是同一个人脸
输入是一个三元组<a,p,n>
- a: anchor
- p: positive , 与a是同一类别的样本
- n: negative , 与a是不同类别的样本
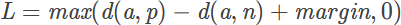
最小化L,则d(a,p)->0,d(a,n)->margin
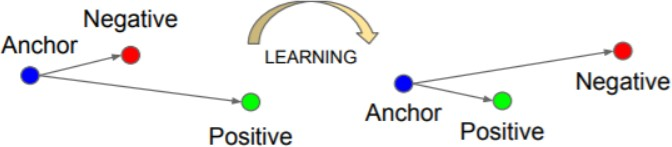
三元组分为以下三个类别:
- easy triplets:可以使loss为0的三元组,即容易分辨的三元组。
- hard triplets:d(a,n)<d(a,p),即一定会误识别的三元组。
- semi-hard triplets:d(a,p)<d(a,n)<d(a,p)+margin,即处在模糊区域的三元组。
semi-hard triplets对我们训练非常重要。
训练方法
1.offline
训练集所有数据经过计算得到对应的embedding,可以得到多个三元组,然后计算triplet loss。
效率不高,因为一次要过一遍所有的数据。
2.online
只计算batch中的triplets,实际中采用这种方法,又分为两种策略,假设B=P*K,P指P个人,每个人有K张图片。
Batch All:计算batch_size中所有valid的hard triplet和semi-hard triplet,然后去平均得到loss。可以产生PK(K-1)(PK-K)个三元组。
Batch Hard:对于每一个anchor,选择距离最大的正样本和距离最小的负样本,共有PK个三元组。
Triplet loss通常是在个体级别的细粒度识别上应用,传统的分类是花鸟狗的大类别的识别,但是有些需求要精确到个体级别,比如精确到哪一个人的人脸识别,所以triplet loss的最主要应用也就是face identification、person re-identification、vehicle re-identification的各种identification问题上。
L1正则化和L2正则化
L1正则化容易使得参数更新时变成0,得到稀疏化的权重,降低模型复杂度,L1正则化有助于选择重要的特征,并将其余特征变为零
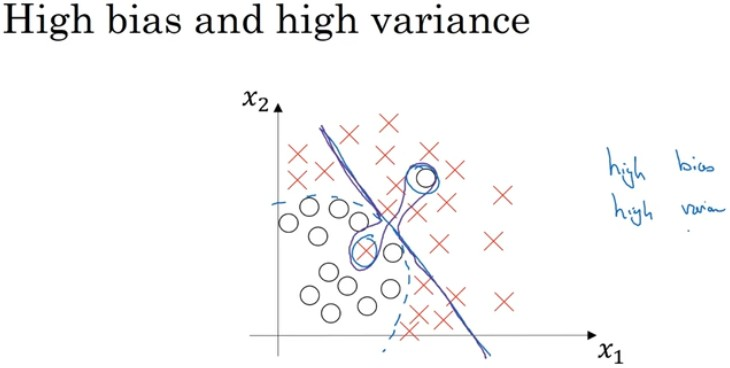
L2正则化容易使得参数更新时值变得很小,得到一个相对平滑的权重,降低模型结构风险防止过拟合方差和偏差
和optimal (base) error相比,比如一般按人类的准确率
偏差 high bias -> underfitting ->Trainset error
方差 high variance -> overfitting -> Dev set error
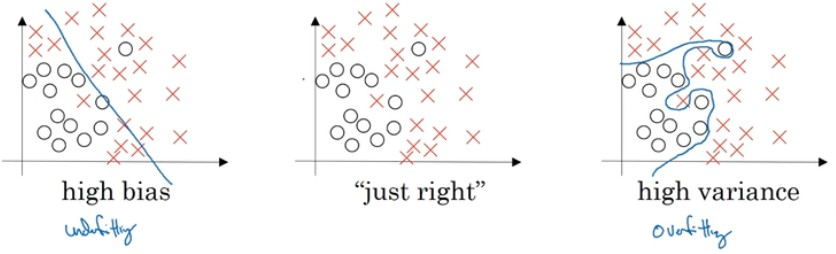
- SGD和Adam的优劣:(总结优化器发展)
SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam
优化器框架:
步骤3、4对于各个算法都是一致的,主要的差别就体现在1和2上
1.SGD
先来看SGD。SGD没有动量的概念,也就是说: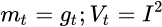
代入步骤3,可以看到下降梯度就是最简单的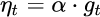
SGD最大的缺点是下降速度慢,而且可能会在沟壑的两边持续震荡,停留在一个局部最优点,梯度为0而无法下降。

1 | # SGD伪代码 |
2.SGD with Momentum
为了抑制SGD的震荡,SGDM认为梯度下降过程可以加入惯性。下坡的时候,如果发现是陡坡,那就利用惯性跑的快一些。SGDM全称是SGD with momentum,在SGD 基础上引入了一阶动量: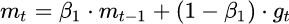
一阶动量是各个时刻梯度方向的指数移动平均值,也就是说,t时刻的下降方向,不 仅由当前点的梯度方向决定,而且由此前累积的下降方向决定,β1的经验值为0.9或0.99,这就意味着下降方向主要是此前累积的下降方向,并略微偏向当前时刻的下降方向。这样可以更快收敛,在鞍点即使梯度为0,仍然可以下降。
1 | # SGDM伪代码2 |
3.SGD with Nesterov Acceleration
SGD还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地,四周都是略高的小山,你觉得没有下坡的方向,那就只能待在这里了。可是如果你爬上 高地,就会发现外面的世界还很广阔。因此,我们不能停留在当前位置去观察未来的 方向,而要向前一步、多看一步、看远一些。
NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进,改进点在于步骤1。我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了 一步,那个时候再怎么走,因此,NAG在步骤1,不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:
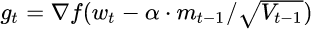
然后用下一个点的梯度方向,与历史累积动量相结合,计算步骤2中当前时刻的累积动量。
4.AdaGrad
以上的几种优化方法都只用到了一阶动量。但是没有考虑到的是,对于经常更新的参数,我们希望学习率低一些,对于不经常更新的参数,我们希望学习率大一些,为此 引入了自适应学习率的优化算法。
二阶动量的出现,才意味着“自适应学习率”优化算法时代的到来,那就是二阶动量—— 该维度上,迄今为止所有梯度值的平方和: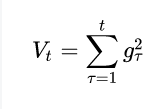
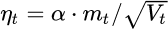
AdaGrad优化算法记录梯度的累积值,梯度累积越大,学习率越小。
1 | # AdaGrad伪代码 |
缺点:因为AdaGrad的学习率是单调递增的,会使得学习率逐渐趋向于0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。
5.AdaDelta/RMSProp
由于AdaGrad单调递减的学习率变化过于激进,我们考虑一个改变二阶动量计算方法的策略:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。
修改的思路很简单。前面我们讲到,指数移动平均值大约就是过去一段时间的平均 值,因此我们用这一方法来计算二阶累积动量: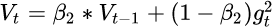
1 | # RMSProp伪代码 |
6.Adam
谈到这里,Adam和Nadam的出现就很自然而然了——它们是前述方法的集大成者。我们看到,SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD 基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了
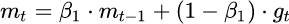
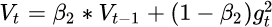
$\beta1 \beta2$两个超参数控制一阶动量和二阶动量1
2
3
4
5
6
7
8
9
10
11
12# Adam伪代码
first_moment = 0
second_moment = 0
for t in range(num_iterations):
dx = gradient(x)
first_moment = beta1 * first_moment + (1 - beta1) * dx
second_moment = beta2 * second_moment + (1 - beta2) * dx
* dx
first_unbias = first_moment / (1 - beta1 ^ t)
second_unbias = second_moment / (1 - beta2 ^ t) # 防止刚开始训练时second_moment很小产生很大的学习率。
x -= learning_rate * first_unbias / (np.sqrt(second_unbias + 1e-7))
Adam优化算法一般取beta1=0.9,beta2=0.999,learning_rate=1e-3或5e-4。
7.Nadam
最后是Nadam。我们说Adam是集大成者,但它遗漏了Nesterov,按照NAG的步骤
1: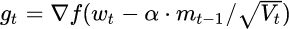
这就是Nesterov + Adam = Nadam了。
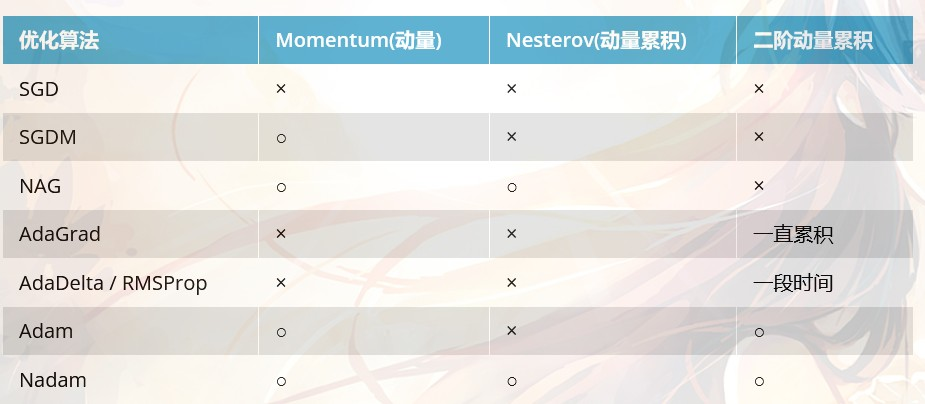
Adam两宗罪:
1.可能不收敛
SGD没有用到二阶动量,因此学习率是恒定的(实际使用过程中会采用学习率衰减 策略,因此学习率递减)。AdaGrad的二阶动量不断累积,单调递增,因此学习率是单调递减的。因此,这两类算法会使得学习率不断递减,最终收敛到0,模型也得以收敛。
但AdaDelta和Adam则不然。二阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的数据可能发生巨变,使得$V_t$可能会时大时小,不是单调变化。这就可能 在训练后期引起学习率的震荡,导致模型无法收敛。
由于Adam中的学习率主要是由二阶动量控制的,为了保证算法的收敛,可以对二阶动量的变化进行控制,避免上下波动。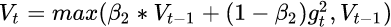
保证$||Vt||\geq||V{t-1}||$从而使得学习率单减
2.可能错过全局最优
数据更重要,不同数据下可能有不同适合的优化算法
优化算法的选择与使用策略:
主流的观点认为:Adam等自适应学习率算法对于稀疏数据具有优势,且收敛速度很快;但精调参数的SGD(+Momentum)往往能够取得更好的最终结果。
先用Adam快速下降,再用SGD调优
切换之后的学习率计算
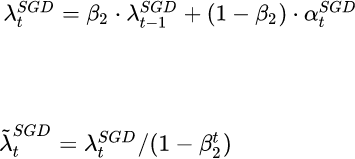

具体内容参考博客:https://blog.csdn.net/S20144144/article/details/103417502
- 增加感受野的方法
1.增加网络层数
2.pooling,SPP结构
3.空洞卷积dilated conv
从字面上就很好理解,是在标准的 convolution map 里注入空洞,以此来增加reception field
图像分割FCN中有两个关键,一个是pooling减小图像尺寸增大感受野,另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中,肯定有一些信息损失掉了,那么能不能设计一种新的操作,不通过pooling也能有较大的感受野看到更多的信息呢?答案就是dilated conv。
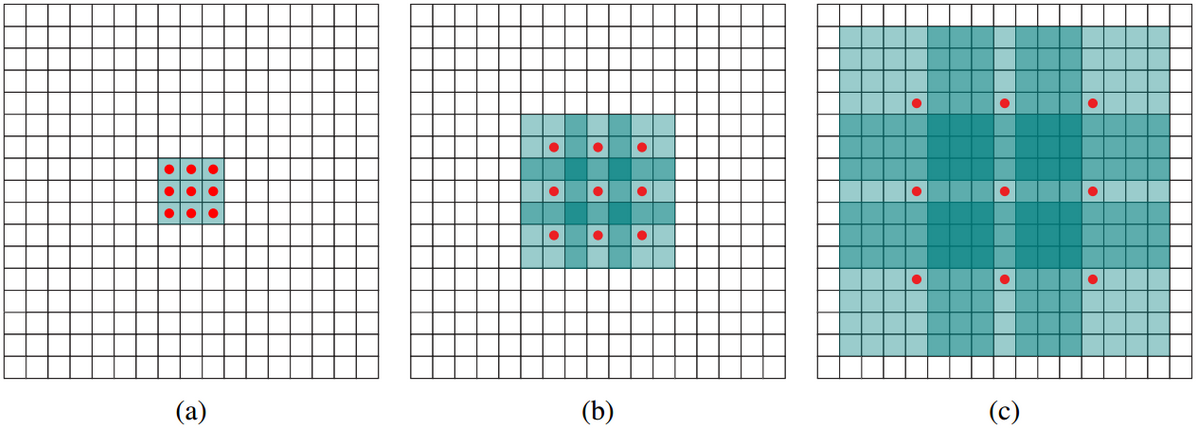
4.可形变卷积deformable conv
添加了位移变量,这个变量根据数据的情况学习,偏移后,相当于卷积核每个方块可 伸缩的变化,从而改变了感受野的范围,感受野成了一个多边形。
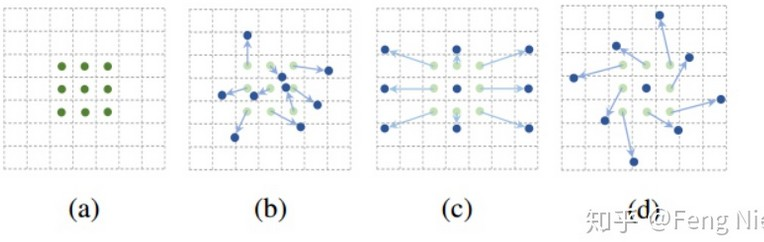
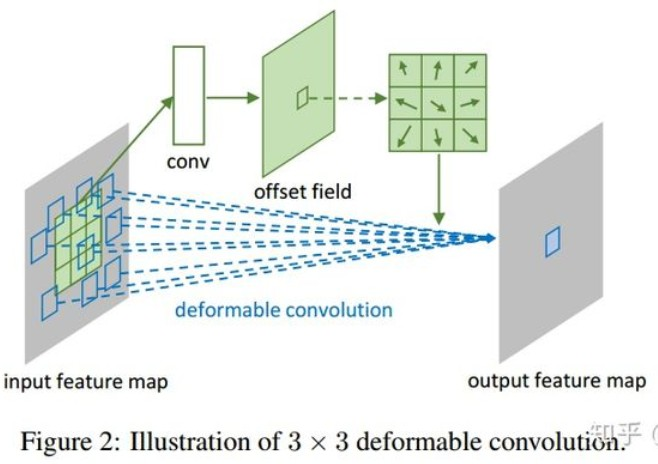
如上图所示,有一个额外的conv层来学习offset,共享input feature maps。然后input feature maps和offset共同作为deformable conv层的输入,deformable conv层操作采样点发生偏移,再进行卷积。
标准卷积可用下面的式子表示:
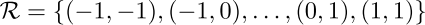
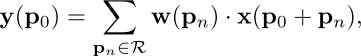
即在标准的3x3的9个位置采样,也就是 $x(p_0+p_n)$,然后每个位置乘卷积核的对应位置权重$w(p_n)$
可形变卷积会学习采样的偏移offset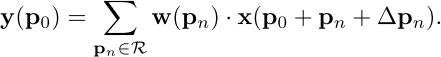
即 ,由于加完offset可能是小数,所以使用双线性插值的方法求解$x(p)$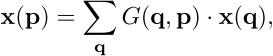
q就是枚举特征图上所有的位置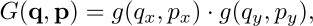
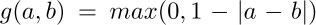
注意,offset预测是预测feature map上每个位置的偏移而不是预测卷积核的偏移, 即输出的offset大小和feature map大小相同,使用相同的卷积核计算得到
而deformable RoI Pooling是先生成pooled feature map然后送到fc层计算每个bin的偏移,然后在重新利用偏移计算pooling
- 深度可分离卷积
分成Depthwise conv和Pointwise conv depthwise conv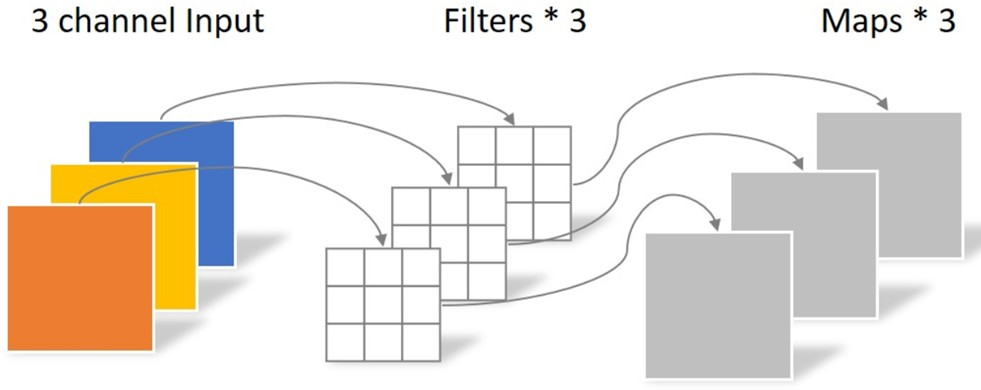
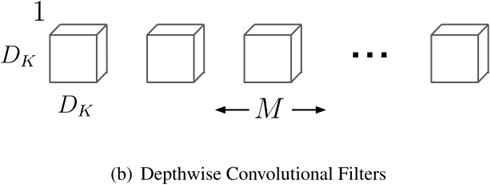
pointwise conv
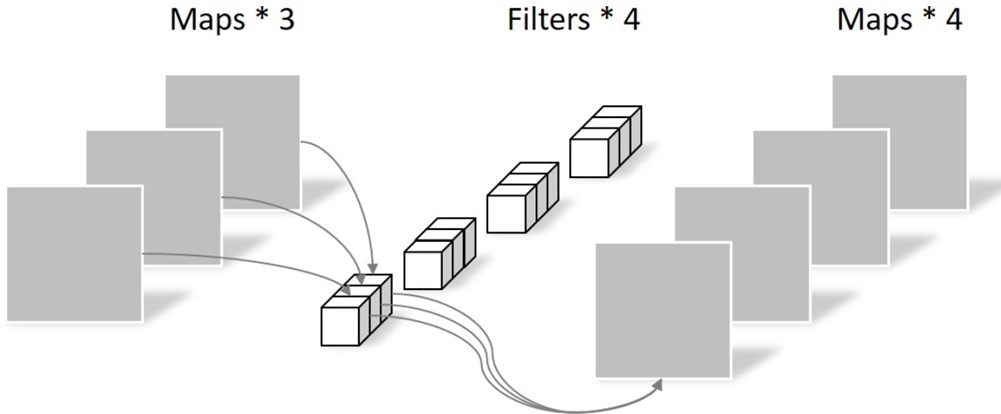
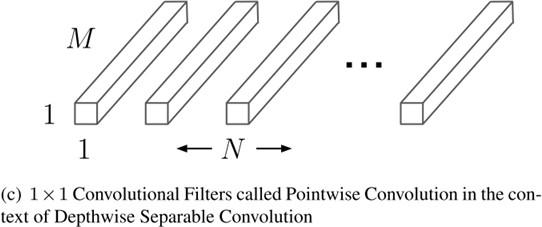
v2提出先1x1进行channel的升维再卷积可以减少信息流失
- ResNet提出残差结构的作用
随着网络层数增加出现,会出现梯度爆炸或梯度消失,另外出现网络退化,即随着层数增加网 络表现先增加至饱和,然后迅速下降。
梯度消失/爆炸的问题可以通过标准初始化和BN层解决
但是网络退化不是过拟合导致的,如果对于一个K层网络是当前最优网络,那么如果构造一个 更深的网络让后面的层学习恒等映射应该至少取得一样的结果而不会更差。但是对网络而言学习恒等映射不容易拟合,但是如果是学习残差,让残差学习为0时即为恒等映射,这样会更容易。这样确保网络表现不受影响甚至很多时候可以提高效果
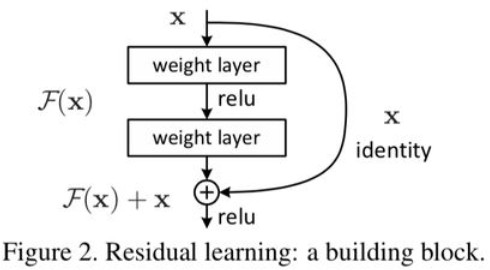
- 1x1卷积核的作用
可以当成是全连接网络,对于每个position,将channel个元素变成filter数个元素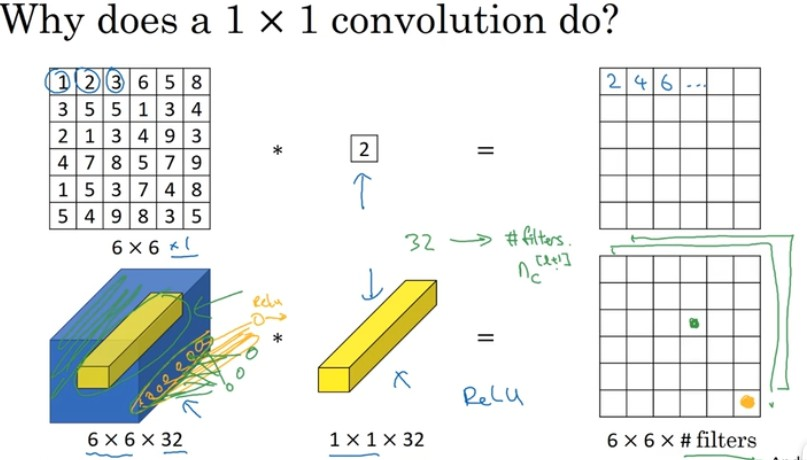
实现跨通道信息的交互和整合
可用于降维,减少计算量,如resnet的bottleneck结构,或升维如mobilenetv2 增加非线性映射的次数
- 数据集分布不平衡的解决办法
1.重采样
可以对多数样本降采样,对少数样本过采样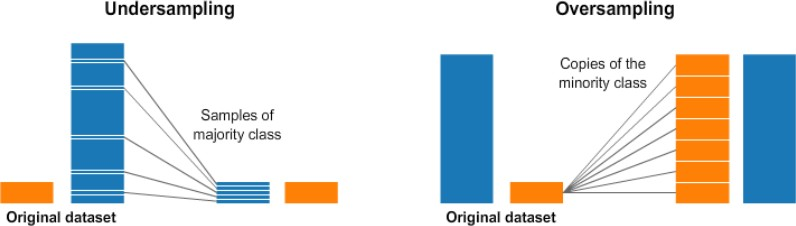
但是问题也很明显,过采样会对少数样本过渡捕捞,而降采样则会损失大量信息
2.hard negative mining,focal loss(balance parameter,focal parameter), loss权重(对少样本预测错误增大惩罚)
3.模型融合
4.评估指标使用F1 score,AUC,ROC等 - F1 Score
- ROC曲线与AUC
AUC (Area under Curve)指ROC曲线下的面积
二分类任务中,比如预测一个人是否还贷款的概率,概率越大还的可能性越大,但是需要设定一个阈值,大于多少概率认为他会还,比如设置为0.35,那么下图虚线上面的样本就被预测为还,下面的样本预测为不还
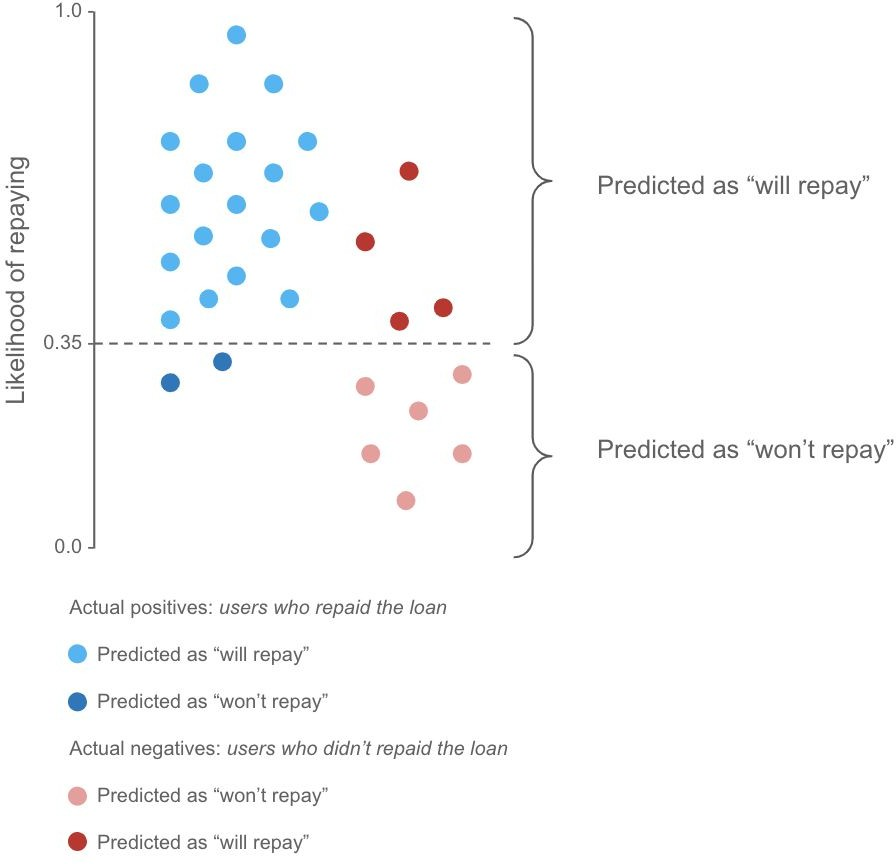
这个时候可以得到一个混淆矩阵

然后利用这个混淆矩阵,计算真阳性率(True Positive Rate, TPR)也称为Recall,
$TPR= \frac{TP}{P}=\frac{TP}{TP+FN}$ ,也就是真正还贷款的人里多少我预测对了,还会计算假阳性率(False Positive Rate, FPR), ,也就是实际没还贷款的人中多少我给预测成还贷款了,这个时候真阳性率为纵轴,假阳性率为横轴,我们不断改变分类的阈值,从0-1,分别计算横纵坐标值画在图上就是ROC曲线
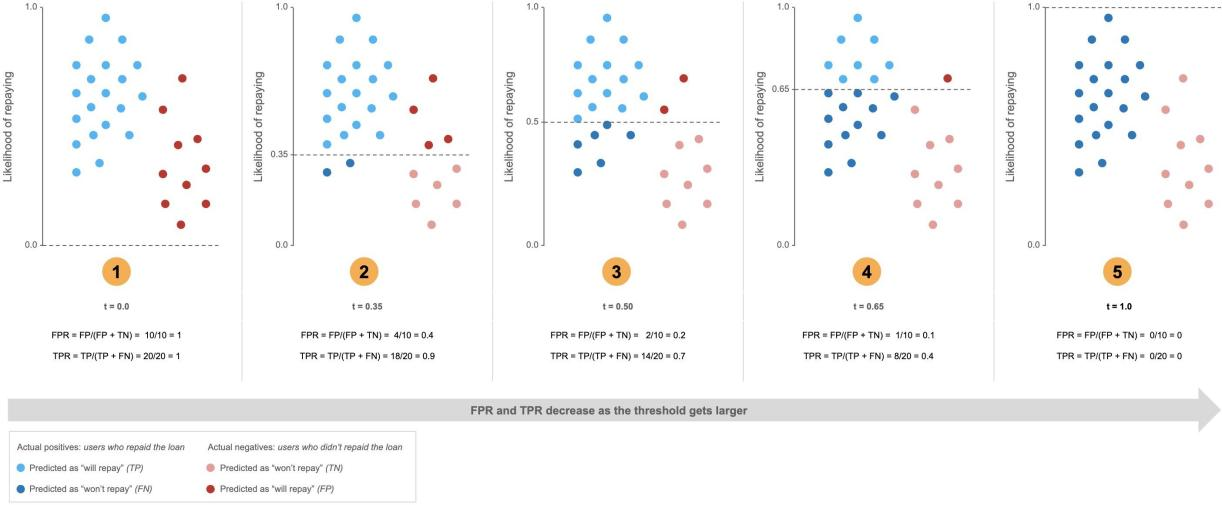
阈值为0时点在图像右上角(1,1),阈值为1时点在图像左下角(0,0)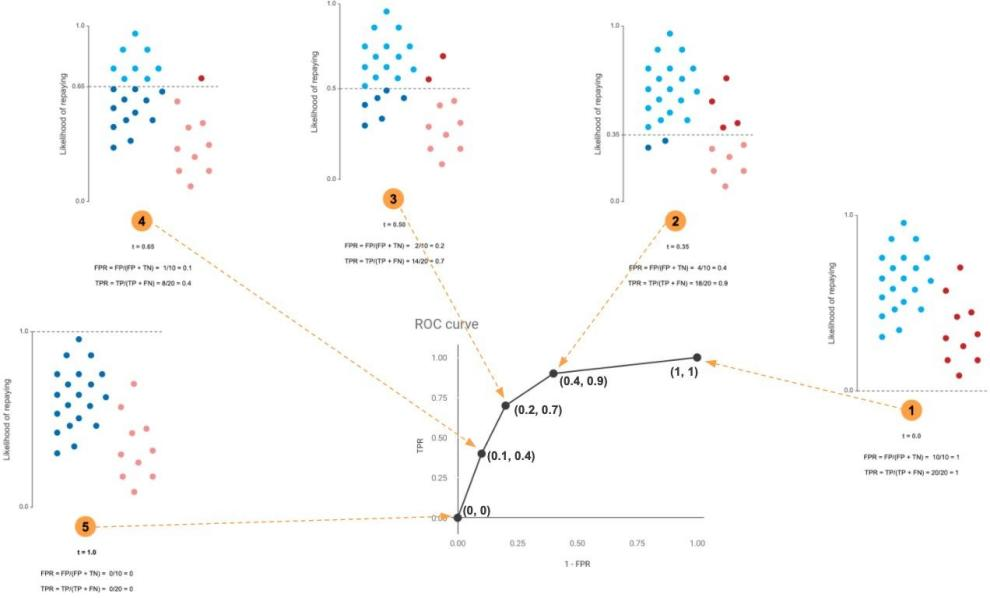
想象一下,如果我的分类器牛逼到预测的和gt一样,那么正样本概率都预测为1,负样本概率 都预测为0,那么阈值在0-1之间无论如何改变,都不会影响横纵坐标的值,只会在阈值设为1 的时候突变,此时的ROC曲线就像下图红色线一样,AUC为1,如果我的模型拉到相当于随机预测,那么相当于上面我们的数据点完全混在一起不可分,此时横纵坐标值会同步变化,那么ROC曲线就是下图的灰色线,AUC为0.5,此时模型毫无意义。
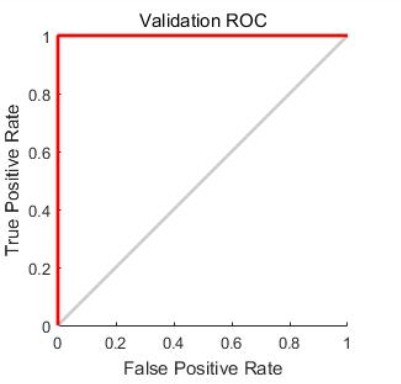
实际计算方法最简单的可以从大到小排个序,然后依次遍历,相当于让每个预测概率作为阈 值,计算面积累加,类似微分思想
另外一种简便的等价计算是,AUC的含义等价于随机挑选一个正样本以及一个负样本,当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。AUC值越大,当前的分类算法越有可能将正样本排在负样本前面,即能够更好的分类。
做N次随机试验,每次实验中随机采样一个正样本和一个负样本,当模型预测正样本的分数大 于模型预测负样本的分数,计数则加1。记计数最终为n(n肯定小于等于N),那么用n/N即得到AUC。
同时又可以等价于下面的计算公式
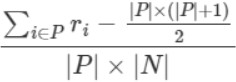
P表示正样本集合,N表示负样本集合。ri表示元素i在全集(P+N)中按预测score从小到大排 的rank位置(rank位置从1开始,比如:假设|P+N|=10,那么最高分的rank值为10,最低分 的rank值为1)。
可以这样想,设从小到大排序, 第一个正样本设为 rank_1, 排在它前面的样本全是负样本,有rank_1-1 个, 对于第二个正样本,设为 rank_2, 那么排在它前面的负样本有 rank_2-2 个,对第 M 个正样本,因为其前面有总共有 rank_M-1 个样本,且已知有 M-1 个是正样本, 故排在它前面的负样本个数为 (rank_M-1)-(M-1)= rank_M-M 个,最后求和就是上面公式的分子,分母是所有可能的pair数。
参考博客:
https://blog.csdn.net/qq_43827595/article/details/120843442
https://blog.csdn.net/weixin_41362649/article/details/89081651
- mAP计算
mAP (mean Average Precision)是各类AP的平均值某一类的AP指该类的P-R曲线下的面积
而该类的P-R曲线指该类别检测Precision-Recall曲线,纵坐标Precision,横坐标Recall
计算过程详解视频:https://www.bilibili.com/video/BV1ez4y1X7g2?from=search&seid=51 91314835491417824&spm_id_from=333.337.0.0
那么具体计算该类的Precision和Recall的方法就是首先把该类的预测框和gt框都提出来,然后 计算TP预测框和gt框的IOU>0.5的个数,FP即IOU<0.5的检测框数量,TP+FP为预测框数量, 之后预测个数TP+FP是根据阈值变化动态变化的,即我设置了阈值,只有高于阈值的才会保留下来作为预测的框,其他就相当于消失,gt个数是静态的,而TP+FP需要对每个阈值动态求
然后TP/gt个数=Recall,TP/预测个数=Precision
对于某一类具体计算时,首先根据IOU计算好是TP还是FP,相当于说我目前先不管阈值,或者说我目前阈值设置为0,所有这些框我不管预测的score先都保留下来了然后计算出所有的TP,FP,然后我对这些框按照score从大到小排序,依次遍历,每遍历到一个数,就相当于把这 个score当成阈值,大于等于这个数的保留,后面的即小于这个数的(因为从大到小排序了) 就当成是消失了我们不管了。对于前面这些,我们累加刚才求好的TP,FP个数即可得到TP,FP。
此时求Precision时的预测框的个数为TP+FP,千万不要以为是原本预测框的个数(因为那个时 候相当于阈值为0),而求Recall时gt个数就还是gt总个数不会变。
计算AP面积时,还是会按照之前排好序的这个顺序,从左到右计算微分面积然后累加,计算时 相同的recall值只计算一遍,每个小矩形的面积时当前recall值减上一个recall值,而当前的高度是从当前位置到后面的最大precision值,这个可以从右往左先预处理出来。
求mAP代码可看pytorch-retinanet源码的eval部分

- IOU loss,GIOU loss,DIOU loss,CIOU loss
参考视频:https://www.bilibili.com/video/BV1yi4y1g7ro?p=4
IOU Loss觉得直接用L2损失不能反映预测框和gt框的重合程度,所以用1-IOU作为loss,这样能反映重合程度也具有尺度不变性,然而如果gt和预测框不相交时IOU恒为零,不能反映距离了
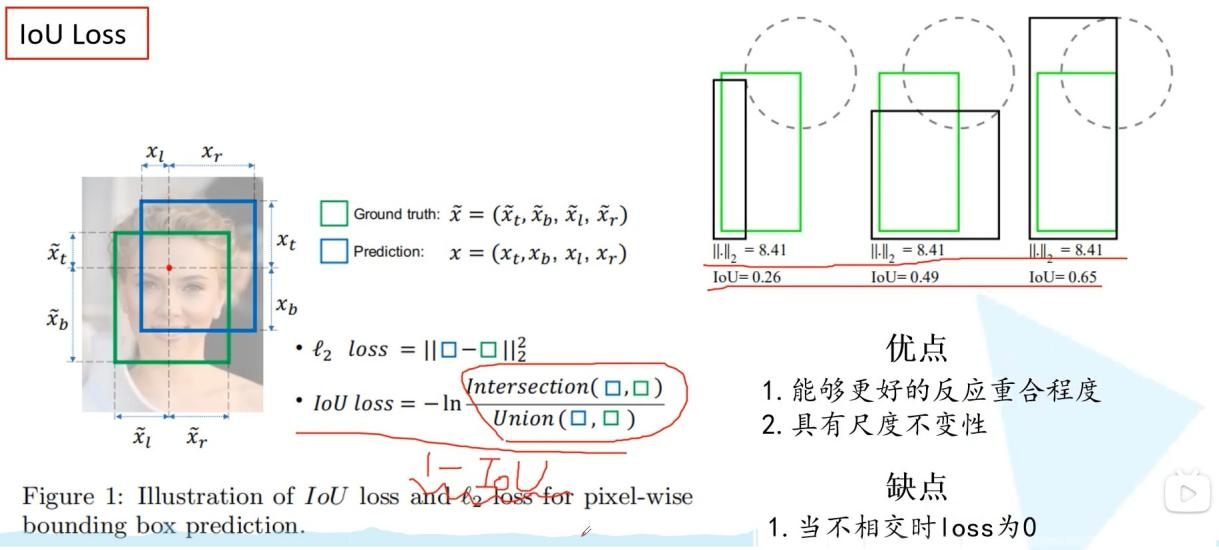
GIOU loss首先计算GIOU,然后loss是1-GIOU
GIOU是IOU-后面的部分Ac是两个框的最小外接矩形面积,u是并集面积,如果两个框完美重合,后面部分是0,则退化成IOU,且IOU=1,两个框无限远时,后面部分趋近于1,IOU为0
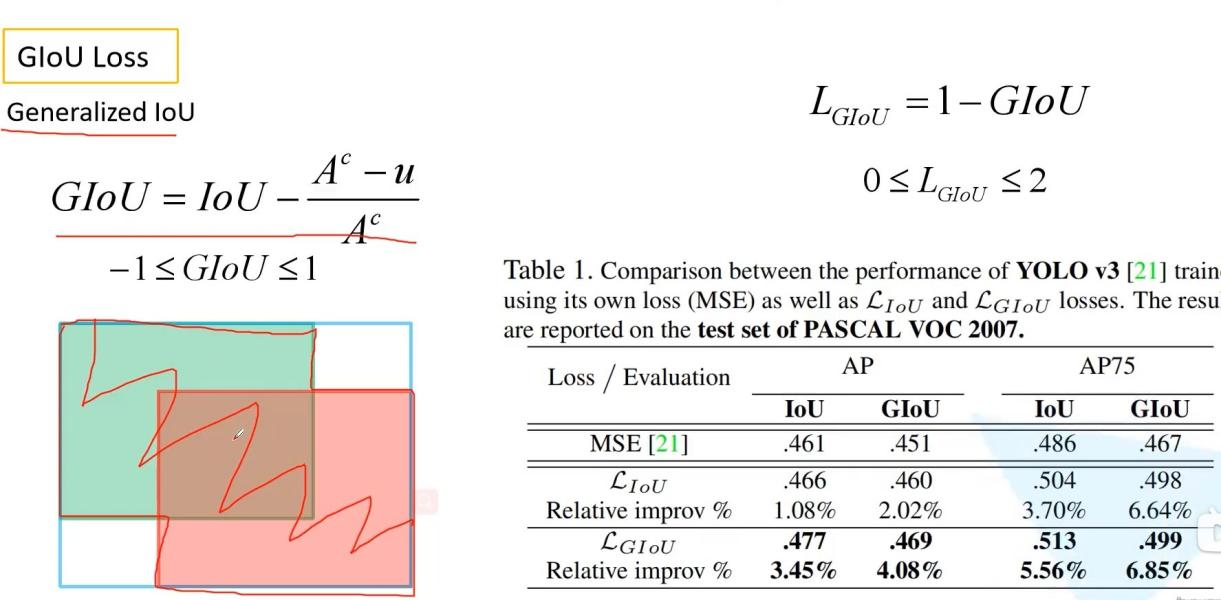
DIOU loss是首先计算DIOU,然后1-DIOU为loss
考虑了中心点距离和最小外接矩形对角线距离的比,收敛速度更快
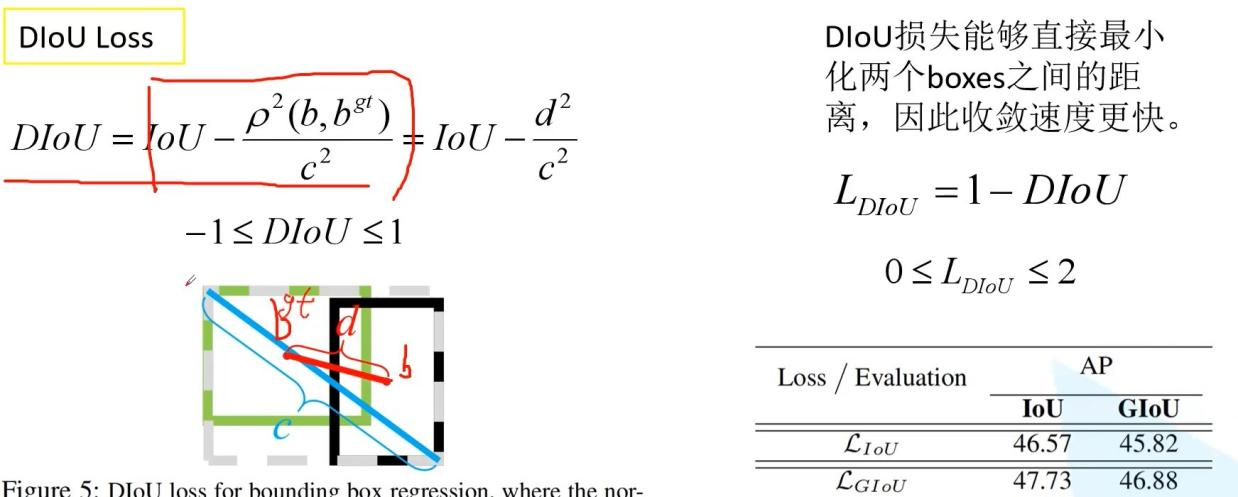
CIOU loss是计算CIOU然后1-CIOU作为loss,在DIOU的基础上有考虑了长宽比因素,比较复杂


多尺度的好处
深层网络的感受野比较大,语义信息表征能力强,但是特征图的分辨率低,几何信息的表征能 力弱(空间几何特征细节缺乏);
低层网络的感受野比较小,几何细节信息表征能力强,虽然分辨率高,但是语义信息表征能力 弱。
目标检测中,不同尺度特征可以对应不同大小的目标,对不同scale的目标效果更好Softmax类别过多怎么办
负采样,层级softmax 详细内容大家自行了解
关于Python
- 变量内存相关
- 变量是标注(类似java的引用),而不是盒子,因此可以为一个对象贴多个标签,仅仅是别名,修改时修改的是同一个对象
==运算符比较两个对象的值,is比较对象的标识- 元组是相对不可变的,即值它保存内容的引用不可变,但是与引用对象无关,例如元 组里有列表,那么只要列表引用不变即可,可以往列表里加元素
- str,byte,array.array是扁平的,保存的不是引用,是在连续内存中保存数据本身
- python默认做浅复制,copy模块的deepcopy可以做深复制
- python的函数传参的唯一支持模式是共享传参,相当于传引用
- del语句只删除名称,不会删除对象,但是可能导致对象被垃圾回收,仅当删除的变量是该对象的最后一个引用
- python垃圾回收机制,CPython垃圾回收使用的主要算法是引用计数,当引用计数 归零,对象会被立即销毁。
- 装饰器和闭包
函数装饰器用于在源码中“标记”函数,以某种方式增强函数的行为
装饰器是可调用的对象(或者想象成一个函数,因为函数在python中也是对象,所以说它是 可调用对象没毛病),其参数是另一个函数(被装饰的函数)。装饰器可能会处理被装饰的函 数,然后把它返回,或者将其替换成另一个函数或可调用对象。
装饰器的一大特性是,能把被装饰的函数替换成其他函数。第二个特性是,装饰器在加载模块 时立即执行。
函数装饰器在导入模块时立即执行,而被装饰的函数只在明确调用时运行。这突出了 Python
程序员所说的导入时和运行时之间的区别
变量作用域规则:
Python 不要求声明变量,但是假定在函数定义体中赋值的变量是局部变量如果在函数中赋值时想让解释器把 b 当成全局变量,要使用 global 声明闭包:
函数中定义函数,内部定义的函数能访问定义体之外定义的非全局变量,即在外部函数内定义 的变量
闭包示例

综上,闭包是一种函数,它会保留定义函数时存在的自由变量的绑定,这样调用函数时, 虽然定义作用域不可用了,但是仍能使用那些绑定
nonlocal
使用nonlocal将变量标记为自由变量,函数内部变量赋值导致变量变成局部变量而不能使用闭包
编程题或思考题
- 模拟大数减法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39// 大数减法
const int L = 110;
string bigSub(string a, string b) { // 假设a > b
string ans;
int na[L] = {0};
int nb[L] = {0};
int la = a.size();
int lb = b.size();
// 倒序存储
for (int i = 0; i < la; i++) { na[la - i - 1] = a[i] - '0'; }
for (int i = 0; i < lb; i++) { nb[lb - i - 1] = b[i] - '0'; }
int lmax = max(la, lb);
// 从个位开始相减
for (int i = 0; i < lmax; i++) {
na[i] -= nb[i];
while (na[i] < 0) {
na[i] += 10;
na[i + 1]--;
}
}
// 处理前置0
while (lmax >= 0 && !na[lmax]) lmax--;
if (lmax < 0) {
ans = "0";
} else {
for (int i = lmax; i >= 0; i--) {
ans += na[i] + '0';
}
}
return ans;
}
拓展:
- 模拟大数减法
1 | const int L = 110; |
大数乘法
一个数的第i 位和另一个数的第j 位相乘所得的数,一定是要累加到结果的第i+j 位上。这里i,j
都是从右往左,从0 开始数。
即:ans[i+j] = a[i]*b[j];最后统一处理进位。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49const int L = 110;
string bigMul(string a, string b) { // 假设a,b为非负整数
string ans;
int x[L] = {0};
int y[L] = {0};
int z[2 * L] = {0};
int la = a.size();
int lb = b.size();
// 倒序存储
for (int i = 0; i < la; i++) {
x[la - i - 1] = a[i] - '0';
}
for (int i = 0; i < lb; i++) {
y[lb - i - 1] = b[i] - '0';
}
// 逐位相乘
for (int i = 0; i < la; i++) {
for (int j = 0; j < lb; j++) {
z[i + j] += x[i] * y[j];
}
}
// 统一进位
for (int i = 0; i < 2 * L; i++) {
if (z[i] >= 10) {
z[i + 1] += z[i] / 10;
z[i] %= 10;
}
}
int lmax = 2 * L - 1;
// 处理前置0
while (lmax >= 0 && !z[lmax]) lmax--;
if (lmax < 0) {
ans = "0";
} else {
for (int i = lmax; i >= 0; i--) {
ans += z[i] + '0';
}
}
return ans;
}大数除法
除法操作不是模仿手工除法,而是利用减法操作实现的。
其基本思想是反复做除法,看从被除数里面最多能减去多少个除数,商就是多少1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
using namespace std;
const int L = 110;
int sub(int *a, int *b, int La, int Lb) {
if (La < Lb) return -1;//如果a小于b,则返回-1
if (La == Lb) {
for (int i = La - 1; i >= 0; i--)
if (a[i] > b[i]) break;
else if (a[i] < b[i]) return -1;//如果a小于b,则返回-1
}
for (int i = 0; i < La; i++)//高精度减法
{
a[i] -= b[i];
if (a[i] < 0) a[i] += 10, a[i + 1]--;
}
for (int i = La - 1; i >= 0; i--)
if (a[i]) return i + 1;//返回差的位数
return 0;//返回差的位数
}
string div(string n1, string n2, int nn)//n1,n2是字符串表示的被除数,除数,nn是选择返回商还是余数
{
string s, v;//s存商,v存余数
int a[L], b[L], r[L], La = n1.size(), Lb = n2.size(), i, tp = La;//a,b是整形数组表示被除数,除数,tp保存被除数的长度
fill(a, a + L, 0);
fill(b, b + L, 0);
fill(r, r + L, 0);//数组元素都置为0
for (i = La - 1; i >= 0; i--)a[La - 1 - i] = n1[i] - '0';
for (i = Lb - 1; i >= 0; i--)b[Lb - 1 - i] = n2[i] - '0';
if (La < Lb || (La == Lb && n1 < n2)) {
//cout<<0<<endl;
return n1;
}//如果a<b,则商为0,余数为被除数
int t = La - Lb;//除被数和除数的位数之差
for (int i = La - 1; i >= 0; i--)//将除数扩大10^t倍
if (i >= t) b[i] = b[i - t];
else b[i] = 0;
Lb = La;
for (int j = 0; j <= t; j++) {
int temp;
while ((temp = sub(a, b + j, La, Lb - j)) >= 0)//如果被除数比除数大继续减
{
La = temp;
r[t - j]++;
}
}
for (i = 0; i < L - 10; i++)r[i + 1] += r[i] / 10, r[i] %= 10;//统一处理进位
while (!r[i]) i--;//将整形数组表示的商转化成字符串表示的
while (i >= 0) s += r[i--] + '0';
//cout<<s<<endl;
i = tp;
while (!a[i]) i--;//将整形数组表示的余数转化成字符串表示的</span>
while (i >= 0) v += a[i--] + '0';
if (v.empty()) v = "0";
//cout<<v<<endl;
if (nn == 1) return s;
if (nn == 2) return v;
}
int main() {
string a, b;
while (cin >> a >> b) {
cout << div(a, b, 1) << endl;
cout << div(a, b, 2) << endl;
}
return 0;
}整数开根号——牛顿迭代法
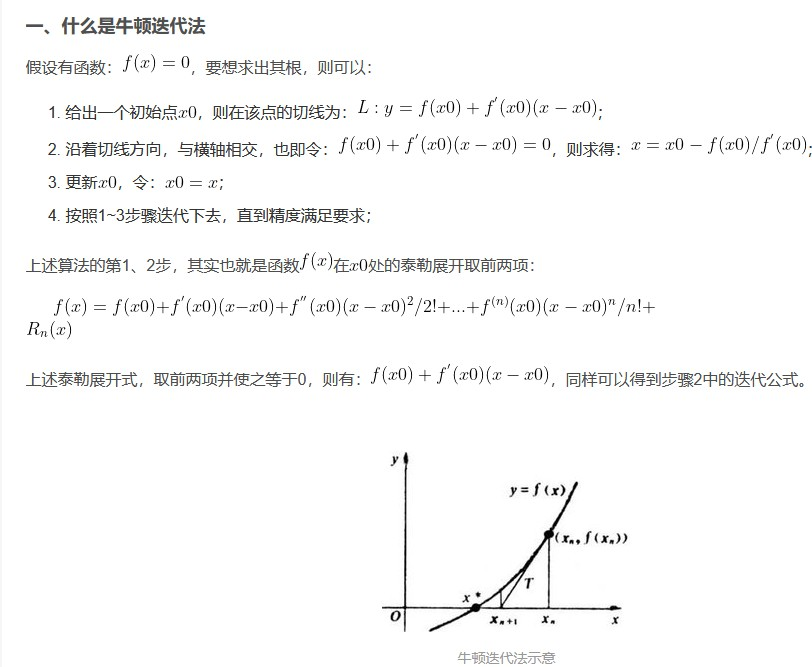

1 | def square_root(n: int) -> float: |
- 快排
python简单实现 时间复杂度和空间复杂度均为$Nlog(N)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17def quicksort(arr):
if not arr:
return []
if len(arr) == 1:
return arr
pivot = arr[0]
left = []
right = []
for i in range(1, len(arr)):
if i <= pivot:
left.append(i)
else:
right.append(i)
return quicksort(left) + [pivot] + quicksort(right)
高效实现
pivot选择
pivot如果选择index=0,那么最差情况是如果序列已经排好序了,那么将花费$N^2$时间复杂度而什么都没做
pivot随机选择最安全,但是随机数生成比较expensive
最佳做法取最左端,最右端和中间位置三个值的中间数(最时髦的)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
using namespace std;
int cutOff = 5;
// 挑选主元
int medianThree(int a[], int left, int right) {
int center = (left + right) / 2;
if (a[left] > a[center])
swap(a[left], a[center]);
if (a[left] > a[right])
swap(a[left], a[right]);
if (a[center] > a[right])
swap(a[center], a[right]);
/* a[left] <= a[center] <= a[right] */
swap(a[center], a[right - 1]);
// left, right位置其实已经分好了一个比pivot小一个比pivot大
// right-1位置是pivot
// 所以只需要对left+1到right-2的数组元素进行处理
return a[right - 1];
}
void insertionSort(int a[], int n) {
int j, p;
for (p = 1; p < n; p++) {
int tmp = a[p];
for (j = p; j > 0 && tmp < a[j - 1]; j--)
a[j] = a[j - 1];
a[j] = tmp;
}
}
// 快排函数
void qSort(int a[], int left, int right) {
int i, j;
int pivot;
if (left + cutOff <= right) {
// 快排核心代码
pivot = medianThree(a, left, right);
i = left;
j = right - 1;
while (1) {
while (a[++i] < pivot);
while (a[--j] > pivot);
if (i < j)
swap(a[i], a[j]);
else
break;
}
swap(a[i], a[right - 1]);
qSort(a, left, i - 1);
qSort(a, i + 1, right);
} else {
insertionSort(a + left, right - left + 1);
}
}
void quickSort(int a[], int n) {
qSort(a, 0, n - 1);
}
int main() {
int a[] = {3, 2, 1, 4, 10, 9, 2, 4};
quickSort(a, 8);
for (int i = 0; i < 8; i++)
cout << a[i] << endl;
return 0;
}
Max Pooling实现
for循环遍历输入feature map尺寸,计算输出output尺寸1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
def max_pooling(inp, kernel_size=3, stride=1, padding=1):
# 获取输入的尺寸
channels = inp.shape[0]
height = inp.shape[1]
weight = inp.shape[2]
# 如果有padding,对input加padding
if padding > 0:
pad_input = np.zeros((channels, height + 2 * padding, weight + 2 * padding)) # 创建新尺寸的数组
pad_input[:, padding: padding + height, padding: padding + weight] = inp # 将原来的input放到中间
inp = pad_input
height += 2 * padding # 更新宽高
weight += 2 * padding
print("padded inp\n", inp)
print("padded inp shape", inp.shape)
output = np.zeros(
(channels, int((height - kernel_size) / stride + 1), int((weight - kernel_size) / stride + 1))) # 计算输出map的尺寸
print("output size", output.shape)
for channel in range(channels): # 遍历input的通道
out_height = 0
for r in range(0, height - kernel_size + 1, stride): # 遍历 input到height-kernel_size+1
out_weight = 0
for c in range(0, weight - kernel_size + 1, stride):
output[channel, out_height, out_weight] = \
np.max(inp[channel, r: r + kernel_size, c: c + kernel_size]) # 取max赋值
out_weight += 1
out_height += 1
return output
inp = np.array([[[1, 2, 3],
[1, 2, 3],
[1, 2, 3]]])
max_pooling(inp, kernel_size=3, stride=2, padding=1)NMS实现
IOU计算方法
通过去两个框左上角的最大值和右下角的最小值计算交集框的左上角和右下角 如果两个框相交则22-11可到的交集框的wh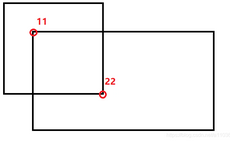
如果不相交22-11为负数,因此去0和22-11的较大值
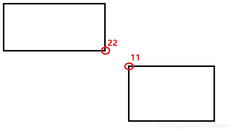
然后计算面积
详细代码如下1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104import numpy as np
"""
np.max(a, axis=None, out=None, keepdims=False)
求a中的最大值
np.maximum:(a, b, out=自定义)
a 与 b 逐位比较取其大者
"""
# nms实现
def nms(dets, thresh):
"""
dets数据格式为 [[xmin, ymin, xmax, ymax, score], ...]
"""
# 获取坐标和分数
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
scores = dets[:, 4]
# 计算每个矩形框的面积
areas = (y2 - y1 + 1) * (x2 - x1 + 1)
# print(areas) # [12321. 29241. 11211. 12321. 8736. 10656.]
# print(scores) # [0.72 0.8 0.92 0.72 0.81 0.9 ]
keep = [] # 用于存放NMS后剩余的框索引
# 取出分数从大到小排列的索引列表
index = scores.argsort()[::-1]
# print(index) # [2 5 4 1 3 0], scores列表没变
while len(index) > 0:
# print(len(index))
# 取出当前第一个框(即分数最大的框)和其他对比
i = index[0]
keep.append(i) # 将这个分数最大的保存
# print(keep)
# print("x1", x1[i]) # x1 220.0
# print(x1[index[1:]]) # [220. 230. 250. 100. 100.]
# 计算第一个框和其余框的交并比
# 计算交集的左上角和右下角
x11 = np.maximum(x1[i], x1[index[1:]]) # 计算i和其余的最大 值,得到一个列表[220. 230. 250. 220. 220.]
y11 = np.maximum(y1[i], y1[index[1:]])
x22 = np.minimum(x2[i], x2[index[1:]])
y22 = np.minimum(y2[i], y2[index[1:]])
# print(x11, y11, x22, y22)
# 计算交集的宽高
w = np.maximum(0, x22 - x11 + 1)
h = np.maximum(0, y22 - y11 + 1)
# 计算交集面积
overlaps = w * h
# print("overlaps is", overlaps) # 计算得到当前i和其余的交集面 积[9696. 8281. 5751. 0. 0.]
# 计算iou,并集面积为两个框的面积相加再减去交集
ious = overlaps / (areas[i] + areas[index[1:]] - overlaps)
# print("ious is", ious) # [0.79664777 0.70984056 0.16573009 0. 0. ]
# 剔除掉iou大于thresh的框,只保留<=thresh的框,使用np.where操作
# idx是需要保留的分数索引,这里的索引是ious列表的索引,而ious列表其实 是去除了当前框的,相对于index索引减了1
# 取[0]是因为返回where操作返回元组(索引,)
idx = np.where(ious <= thresh)[0]
# print(idx)
# 更新剩余的框索引
index = index[idx + 1]
return keep
############################################# 以下为可视化
#################################################
boxes = np.array([[100, 100, 210, 210, 0.72],
[250, 250, 420, 420, 0.8],
[220, 220, 320, 330, 0.92],
[100, 100, 210, 210, 0.72],
[230, 240, 325, 330, 0.81],
[220, 230, 315, 340, 0.9]])
import matplotlib.pyplot as plt
def plot_bbox(dets, c='k'):
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
plt.plot([x1, x2], [y1, y1], c)
plt.plot([x1, x1], [y1, y2], c)
plt.plot([x1, x2], [y2, y2], c)
plt.plot([x2, x2], [y1, y2], c)
plt.title(" nms")
plt.figure(1)
ax1 = plt.subplot(1, 2, 1)
ax2 = plt.subplot(1, 2, 2)
plt.sca(ax1)
plot_bbox(boxes, 'k') # before nms
keep = nms(boxes, thresh=0.7)
plt.sca(ax2)
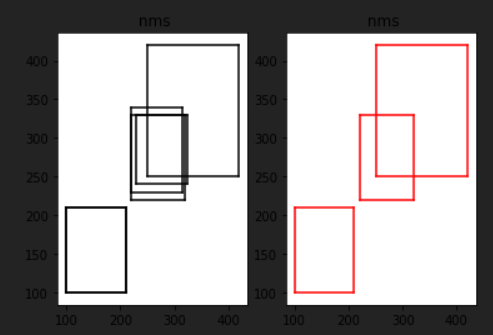
plot_bbox(boxes[keep], 'r') # after nms
可视化结果
- 将$N \times H \times W \times C$的int8数据转成$N \times C\times H\times W\times$的float数据,然后将RGB转成BGR
1 | # 将N X H X W X C的int8数据转成N X C X H X W的float数据 |
Coding——基础编程算法模板
快速幂1
2
3
4
5
6
7
8
9
10
11
12int pow(int a, int b) {
int ans = 1;
a %= mod;
while (b) {
if (b & 1)
ans = ans * a % mod;
b >>= 1;
a = a * a % mod;
}
return ans;
}
并查集模板(本质上就是找连通性的,如果问题可以转换成连通性判断问题,那就可以用并查集)
1 | const int N = 100; // 节点数量 |
1 | inline void init(int n) { |
最短路
Dijkstra 朴素模板$O(n^2)$
1 | // 按秩合并版 |
1 | // 邻接表版本 |
优先队列优化$(V+E)log(V)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
using namespace std;
typedef long long ll;
const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
struct node {
int to, dis;
bool operator<(const node x) const {
return dis > x.dis;
}
};
vector<node> w[maxn];
int dis[maxn], vis[maxn], n;
void dijkstra() {
memset(dis, inf, sizeof(dis));
memset(vis, 0, sizeof(vis));
dis[0] = 0;
priority_queue<node> pq;
node now, ne;
now.to = 0, now.dis = 0;
pq.push(now);
while (!pq.empty()) {
now = pq.top(), pq.pop();
if (vis[now.to])
continue;
vis[now.to] = 1;
for (int i = 0; i < w[now.to].size(); ++i) {
int to = w[now.to][i].to;
if (!vis[to] && dis[to] > now.dis + w[now.to][i].dis) {
dis[to] = now.dis + w[now.to][i].dis;
ne.dis = dis[to];
ne.to = to;
pq.push(ne);
}
}
}
}
int main() {
int m, a, b, c, v, num;
while (~scanf("%d%d", &n, &m)) {
node now;
for (int i = 1; i <= m; ++i) {
scanf("%d%d%d", &a, &b, &now.dis);
now.to = b;
w[a].push_back(now); //vector存边,(数组也可以)
now.to = a;
w[b].push_back(now);
}
dijkstra();
for (int i = 0; i < n; ++i)
printf("%d%c", dis[i], i == n - 1 ? '\n' : ' ');
}
return 0;
}
dijkstra+dfs搜索路径(例题)
1 |
|
弗洛伊德多源最短路1
2
3
4
5
6
7
8
9
10
for(int k = 0;k<n;k++) {
for(int i = 0;i<n;i++) {
for(int j = 0;j<n;j++) {
if(G[i][j] > G[i][k] + G[k][j]) {
G[i][j] = G[i][k] + G[k][j];
}
}
}
}
bellman-ford 判断负环$O(|E||V|)$ ,最多经过k个点,k个边的最短路,每次松弛时复制上次一更新的数组,不要实时更新dis
1 | struct node { |
最小生成树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29// Kruskal 适合给定所有边
int Find(int x) {
if (x == pre[x])
return x;
else return pre[x] = Find(pre[x]);
}
int Kruskal() {
for (int i = 0; i <= n; i++) {
pre[i] = i;
}
int num = 0, sum = 0;
for (int i = 0; i < m; i++) {
int u = Find(edge[i].u);
int v = Find(edge[i].v);
if (u != v) {
pre[u] = v;
num++;
sum += edge[i].w;
}
if (num == n - 1) break;
}
if (num == n - 1) return sum;
else return 0;
}
1 | // prim s |
拓扑排序
每次排入度为0的点,然后去掉这个点,减少指向点的入度,在发现入度为0的点,循环
1 |
|
树的前中后遍历非递归1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
// 前序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x),
left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> preorderTraversal(TreeNode *root) {
stack < TreeNode * > st;
TreeNode *p = root;
vector<int> ans;
while (p || st.size() > 0) {
if (p) {
ans.push_back(p->val);
st.push(p);
p = p->left;
} else {
p = st.top();
st.pop();
p = p->right;
}
}
return ans;
}
};
// 中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x),
left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode *root) {
stack < TreeNode * > st;
TreeNode *p = root;
vector<int> ans;
while (p || st.size() > 0) {
if (p) {
st.push(p);
p = p->left;
} else {
p = st.top();
st.pop();
ans.push_back(p->val);
p = p->right;
}
}
return ans;
}
};
// 后续遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x),
left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> postorderTraversal(TreeNode *root) {
stack < TreeNode * > st;
unordered_map < TreeNode * , int > stflag;
vector<int> ans;
TreeNode *p = root;
while (p || st.size() > 0) {
if (p) {
st.push(p);
stflag[p] = 1;
p = p->left;
} else {
p = st.top();
if (stflag[p] == 1) {
stflag[p] = 2;
p = p->right;
} else {
ans.push_back(p->val);
st.pop();
p = NULL;
}
}
}
return ans;
}
};
归并排序用来求逆序数思路:
合并阶段 本质上是 合并两个排序数组 的过程,而每当遇到 左子数组当前元素 > 右子数组当前元素时,意味着 「左子数组当前元素 至 末尾元素」 与 「右子数组当前元素」 构成了若干 「逆序对」 。
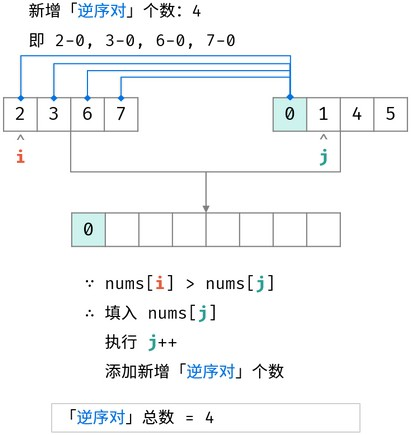
1 | class Solution { |
导入头文件1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using namespace std;
int main() {
return 0;
}
初始化vector1
2
3
4
5// 一维vector
vector<int> vec(4, 0); // size为4,全部初始为0
// 二维vector
vector<vector<int> > vec(m, vector<int>(n, 0)); // mxn全为0
auto for循环map,set,map使用.获取元素1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20// map
map<int, int> mp;
mp[1] = 5;
mp[3] = 4;
mp[7] = 9;
for(auto &i: mp) {
cout << i.first << " " << i.second <<endl;
}
// set
set<int> st;
st.insert(1);
st.insert(5);
st.insert(2);
for(auto &i: st) {
cout << i <<endl;
}
使用iterator遍历1
2
3
4
5map <int, int> :: iterator it;
it->first
it->second
set<int> :: iterator it;
*it
sort比较函数1
2
3
4
5
6
7
8
9
10
11// c++
struct node {
int e1;
int e2;
};
bool cmp(node a, node b) { // 如果在class里面写cmp函数前面加static
return a.e1 < b.e1; // < 升序,从小到大,> 降序 从大到小
}
sort(vec.begin(), vec.end(), cmp);
1 | # python |
初始化
fill函数
1 | // 一维数组 |
memset函数
1 | // 1. memset是以字节为单位,初始化内存块。 |
优先队列1
2priority_queue<int, vector<int>, greater<int>> heap; // 最小堆
priority_queue<int, vector<int>, less<int>> heap; // 最大堆
deque用法